Pendulum (mathematics)

Classical mechanics
${\vec {F}}=m{\vec {a}}$ Second law of motion
History Timeline
Branches Applied Celestial Continuum Dynamics Kinematics Kinetics Statics Statistical
Fundamentals Acceleration Angular momentum Couple D'Alembert's principle Energy kinetic potential Force Frame of reference Impulse Inertia / Moment of inertia Mass Mechanical power Mechanical work Moment Momentum Space Speed Time Torque Velocity Virtual work
Formulations Newton's laws of motion Analytical mechanics Lagrangian mechanics Hamiltonian mechanics Routhian mechanics Hamilton–Jacobi equation Appell's equation of motion Udwadia–Kalaba equation Koopman–von Neumann mechanics
Core topics Damping (ratio) Displacement Equations of motion Euler's laws of motion Fictitious force Friction Harmonic oscillator Inertial / Non-inertial reference frame Mechanics of planar particle motion Motion (linear) Newton's law of universal gravitation Newton's laws of motion Relative velocity Rigid body dynamics Euler's equations Simple harmonic motion Vibration
Rotation Circular motion Rotating reference frame Centripetal force Centrifugal force reactive Coriolis force Pendulum Tangential speed Rotational speed Angular acceleration / displacement / frequency / velocity
Scientists Galileo Newton Kepler Horrocks Halley Euler d'Alembert Clairaut Lagrange Laplace Hamilton Poisson Daniel Bernoulli Johann Bernoulli Cauchy

For a more accessible and less technical introduction to this topic, see Introduction to pendulum (mathematics).

The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allows the equations of motion to be solved analytically for small-angle oscillations.

Simple gravity pendulum

Animation of a pendulum showing the velocity and acceleration vectors.

A so-called "simple pendulum" is an idealization of a "real pendulum" but in an isolated system using the following assumptions:

The rod or cord on which the bob swings is massless, inextensible and always remains taut;
The bob is a point mass;
Motion occurs only in two dimensions, i.e. the bob does not trace an ellipse but an arc.
The motion does not lose energy to friction or air resistance.
The gravitational field is uniform.
The support does not move.

The differential equation which represents the motion of a simple pendulum is

{\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{\ell }}\sin \theta =0

Eq. 1

where $g$ is acceleration due to gravity, $l$ is the length of the pendulum, and $θ$ is the angular displacement.

"Force" derivation of (Eq. 1) Figure 1. Force diagram of a simple gravity pendulum. Consider Figure 1 on the right, which shows the forces acting on a simple pendulum. Note that the path of the pendulum sweeps out an arc of a circle. The angle $θ$ is measured in radians, and this is crucial for this formula. The blue arrow is the gravitational force acting on the bob, and the violet arrows are that same force resolved into components parallel and perpendicular to the bob's instantaneous motion. The direction of the bob's instantaneous velocity always points along the red axis, which is considered the tangential axis because its direction is always tangent to the circle. Consider Newton's second law, $F=ma$ where $F$ is the sum of forces on the object, $m$ is mass, and $a$ is the acceleration. Because we are only concerned with changes in speed, and because the bob is forced to stay in a circular path, we apply Newton's equation to the tangential axis only. The short violet arrow represents the component of the gravitational force in the tangential axis, and trigonometry can be used to determine its magnitude. Thus, ${\begin{aligned}F&=-mg\sin \theta =ma\\a&=-g\sin \theta \end{aligned}}$ where $g$ is the acceleration due to gravity near the surface of the earth. The negative sign on the right hand side implies that $θ$ and $a$ always point in opposite directions. This makes sense because when a pendulum swings further to the left, we would expect it to accelerate back toward the right. This linear acceleration $a$ along the red axis can be related to the change in angle $θ$ by the arc length formulas; $s$ is arc length: ${\begin{aligned}s&=\ell \theta \\v&={\frac {ds}{dt}}=\ell {\frac {d\theta }{dt}}\\a&={\frac {d^{2}s}{dt^{2}}}=\ell {\frac {d^{2}\theta }{dt^{2}}}\end{aligned}}$ thus: ${\begin{aligned}\ell {\frac {d^{2}\theta }{dt^{2}}}&=-g\sin \theta \\{\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{\ell }}\sin \theta &=0\end{aligned}}$

"Torque" derivation of (Eq. 1) Equation (1) can be obtained using two definitions for torque. ${\boldsymbol {\tau }}=\mathbf {r} \times \mathbf {F} ={\frac {d\mathbf {L} }{dt}}$ First start by defining the torque on the pendulum bob using the force due to gravity. ${\boldsymbol {\tau }}=\mathbf {l} \times \mathbf {F} _{\mathrm {g} },$ where $l$ is the length vector of the pendulum and $F g$ is the force due to gravity. For now just consider the magnitude of the torque on the pendulum. $\|{\boldsymbol {\tau }}\|=-mg\ell \sin \theta ,$ where $m$ is the mass of the pendulum, $g$ is the acceleration due to gravity, $l$ is the length of the pendulum and $θ$ is the angle between the length vector and the force due to gravity. Next rewrite the angular momentum. $\mathbf {L} =\mathbf {r} \times \mathbf {p} =m\mathbf {r} \times ({\boldsymbol {\omega }}\times \mathbf {r} ).$ Again just consider the magnitude of the angular momentum. $\|\mathbf {L} \|=mr^{2}\omega =m\ell ^{2}{\frac {d\theta }{dt}}.$ and its time derivative ${\frac {d}{dt}}\|\mathbf {L} \|=m\ell ^{2}{\frac {d^{2}\theta }{dt^{2}}},$ According to $τ = d L / dt$ , we can get by comparing the magnitudes $-mg\ell \sin \theta =m\ell ^{2}{\frac {d^{2}\theta }{dt^{2}}},$ thus: ${\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{\ell }}\sin \theta =0,$ which is the same result as obtained through force analysis.

"Energy" derivation of (Eq. 1) 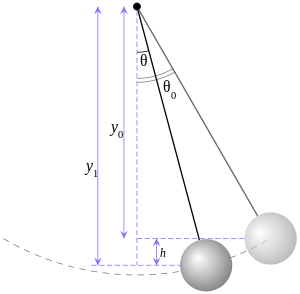Figure 2. Trigonometry of a simple gravity pendulum. It can also be obtained via the conservation of mechanical energy principle: any object falling a vertical distance $h$ would acquire kinetic energy equal to that which it lost to the fall. In other words, gravitational potential energy is converted into kinetic energy. Change in potential energy is given by $\Delta U = mgh\,$ change in kinetic energy (body started from rest) is given by $\Delta K={\tfrac {1}{2}}mv^{2}$ Since no energy is lost, the gain in one must be equal to the loss in the other ${\tfrac {1}{2}}mv^{2}=mgh\,$ the change in velocity for a given change in height can be expressed $v = \sqrt{2gh}\,$ Using the arc length formula above, this equation can be rewritten in terms of $dθ / dt$ ${\begin{aligned}v=\ell {\frac {d\theta }{dt}}&={\sqrt {2gh}}\\{\frac {d\theta }{dt}}&={\frac {\sqrt {2gh}}{l}}\end{aligned}}$ $h$ is the vertical distance the pendulum fell. Look at Figure 2, which presents the trigonometry of a simple pendulum. If the pendulum starts its swing from some initial angle $θ 0$ , then $y 0$ , the vertical distance from the screw, is given by $y_0 = \ell\cos\theta_0\,$ similarly, for $y 1$ , we have $y_{1}=l\cos \theta \,$ then $h$ is the difference of the two $h = \ell\left(\cos\theta-\cos\theta_0\right)$ in terms of $dθ / dt$ gives ${\frac {d\theta }{dt}}={\sqrt {{\frac {2g}{\ell }}(\cos \theta -\cos \theta _{0})}}$ Eq. 2 This equation is known as the first integral of motion, it gives the velocity in terms of the location and includes an integration constant related to the initial displacement ( $θ 0$ ). We can differentiate, by applying the chain rule, with respect to time to get the acceleration ${\begin{aligned}{\frac {d}{dt}}{\frac {d\theta }{dt}}&={\frac {d}{dt}}{\sqrt {{\frac {2g}{\ell }}\left(\cos \theta -\cos \theta _{0}\right)}}\\{\frac {d^{2}\theta }{dt^{2}}}&={\frac {1}{2}}{\frac {-{\frac {2g}{\ell }}\sin \theta }{\sqrt {{\frac {2g}{\ell }}(\cos \theta -\cos \theta _{0})}}}{\frac {d\theta }{dt}}\\&={\frac {1}{2}}{\frac {-{\frac {2g}{\ell }}\sin \theta }{\sqrt {{\frac {2g}{e}}ll(\cos \theta -\cos \theta _{0})}}}{\sqrt {{\frac {2g}{\ell }}(\cos \theta -\cos \theta _{0})}}=-{\frac {g}{\ell }}\sin \theta \\{\frac {d^{2}\theta }{dt^{2}}}&+{\frac {g}{\ell }}\sin \theta =0,\end{aligned}}$ which is the same result as obtained through force analysis.

Small-angle approximation

Small-angle approximation for the sine function: For

θ \approx 0

we find

sin θ \approx θ

The differential equation given above is not easily solved, and there is no solution that can be written in terms of elementary functions. However adding a restriction to the size of the oscillation's amplitude gives a form whose solution can be easily obtained. If it is assumed that the angle is much less than 1 radian (often cited as less than 0.1 radians, about 6°), or

\theta \ll 1,\,

then substituting for $sin θ$ into Eq. 1 using the small-angle approximation,

\sin \theta \approx \theta ,\,

yields the equation for a harmonic oscillator,

{\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{\ell }}\theta =0.

The error due to the approximation is of order $θ 3$ (from the Maclaurin series for $sin θ$ ).

Given the initial conditions $θ (0) = θ 0$ and $dθ / dt (0) = 0$ , the solution becomes

$\theta (t)=\theta _{0}\cos \left({\sqrt {\frac {g}{\ell }}}\,t\right)\quad \quad \quad \quad \theta _{0}\ll 1.$

The motion is simple harmonic motion where $θ 0$ is the amplitude of the oscillation (that is, the maximum angle between the rod of the pendulum and the vertical). The period of the motion, the time for a complete oscillation (outward and return) is

$T_{0}=2\pi {\sqrt {\frac {\ell }{g}}}\quad \quad \quad \quad \quad \theta _{0}\ll 1$

which is known as Christiaan Huygens's law for the period. Note that under the small-angle approximation, the period is independent of the amplitude $θ 0$ ; this is the property of isochronism that Galileo discovered.

Rule of thumb for pendulum length

T_{0}=2\pi {\sqrt {\frac {\ell }{g}}}

can be expressed as

\ell ={\frac {g}{\pi ^{2}}}{\frac {T_{0}^{2}}{4}}.

If SI units are used (i.e. measure in metres and seconds), and assuming the measurement is taking place on the Earth's surface, then $g \approx 9.81 m/s 2$ , and $g / π 2 \approx 1$ (0.994 is the approximation to 3 decimal places).

Therefore, a relatively reasonable approximation for the length and period are,

{\begin{aligned}\ell &\approx {\frac {T_{0}^{2}}{4}},\\T_{0}&\approx 2{\sqrt {\ell }}\end{aligned}}

where $T 0$ is the number of seconds between two beats (one beat for each side of the swing), and $l$ is measured in metres.

Arbitrary-amplitude period

For amplitudes beyond the small angle approximation, one can compute the exact period by first inverting the equation for the angular velocity obtained from the energy method (Eq. 2),

Figure 3. Deviation of the "true" period of a pendulum from the small-angle approximation of the period. "True" value was obtained numerically evaluating the elliptic integral.

Figure 4. Relative errors using the power series for the period.

{\frac {dt}{d\theta }}={\sqrt {\frac {\ell }{2g}}}{\frac {1}{\sqrt {\cos \theta -\cos \theta _{0}}}}

and then integrating over one complete cycle,

T = t(\theta_0\rightarrow0\rightarrow-\theta_0\rightarrow0\rightarrow\theta_0),

or twice the half-cycle

T=2t(\theta _{0}\rightarrow 0\rightarrow -\theta _{0}),

or four times the quarter-cycle

T=4t(\theta _{0}\rightarrow 0),

which leads to

T=4{\sqrt {\frac {\ell }{2g}}}\int _{0}^{\theta _{0}}{\frac {1}{\sqrt {\cos \theta -\cos \theta _{0}}}}\,d\theta .

Note that this integral diverges as $θ 0$ approaches the vertical

\lim _{\theta _{0}\rightarrow \pi }T=\infty ,

so that a pendulum with just the right energy to go vertical will never actually get there. (Conversely, a pendulum close to its maximum can take an arbitrarily long time to fall down.)

This integral can be rewritten in terms of elliptic integrals as

T=4{\sqrt {\frac {\ell }{g}}}F\left({\frac {\theta _{0}}{2}},\csc {\frac {\theta _{0}}{2}}\right)\csc {\frac {\theta _{0}}{2}}

where $F$ is the incomplete elliptic integral of the first kind defined by

F(\varphi ,k)=\int _{0}^{\varphi }{\frac {1}{\sqrt {1-k^{2}\sin ^{2}u}}}\,du\,.

Or more concisely by the substitution

\sin {u}={\frac {\sin {\frac {\theta }{2}}}{\sin {\frac {\theta _{0}}{2}}}}

expressing $θ$ in terms of $u$ ,

T=4{\sqrt {\frac {\ell }{g}}}K(k),k=\sin(\theta _{0}/2)

Eq. 3

where $K$ is the complete elliptic integral of the first kind defined by

K(k)=F\left({\frac {\pi }{2}},k\right)=\int _{0}^{\pi /2}{\frac {1}{\sqrt {1-k^{2}\sin ^{2}u}}}\,du\,.

For comparison of the approximation to the full solution, consider the period of a pendulum of length 1 m on Earth ( $g$ = 9.80665 m/s²) at initial angle 10 degrees is

4{\sqrt {\frac {1{\text{ m}}}{g}}}\ K(\sin {\frac {10^{\circ }}{2}})\approx 2.0102{\text{ s}}.

The linear approximation gives

2\pi {\sqrt {\frac {1{\text{ m}}}{g}}}\approx 2.0064{\text{ s}}.

The difference between the two values, less than 0.2%, is much less than that caused by the variation of $g$ with geographical location.

From here there are many ways to proceed to calculate the elliptic integral.

Legendre polynomial solution for the elliptic integral

Given Eq. 3 and the Legendre polynomial solution for the elliptic integral:

K(k)={\frac {\pi }{2}}\left(1+\left({\frac {1}{2}}\right)^{2}k^{2}+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}k^{4}+\cdots +\left({\frac {(2n-1)!!}{(2n)!!}}\right)^{2}k^{2n}+\cdots \right),

where $n!!$ denotes the double factorial, an exact solution to the period of a pendulum is:

{\begin{alignedat}{2}T&=2\pi {\sqrt {\frac {\ell }{g}}}\left(1+\left({\frac {1}{2}}\right)^{2}\sin ^{2}{\frac {\theta _{0}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}\sin ^{4}{\frac {\theta _{0}}{2}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{2}\sin ^{6}{\frac {\theta _{0}}{2}}+\cdots \right)\\&=2\pi {\sqrt {\frac {\ell }{g}}}\cdot \sum _{n=0}^{\infty }\left(\left({\frac {(2n)!}{(2^{n}\cdot n!)^{2}}}\right)^{2}\cdot \sin ^{2n}{\frac {\theta _{0}}{2}}\right).\end{alignedat}}

Figure 4 shows the relative errors using the power series. $T 0$ is the linear approximation, and $T 2$ to $T 10$ include respectively the terms up to the 2nd to the 10th powers.

Figure 5. Potential energy and phase portrait of a simple pendulum. Note that the

x

-axis, being angle, wraps onto itself after every 2

π

radians.

Power series solution for the elliptic integral

Another formulation of the above solution can be found if the following Maclaurin series:

\sin {\frac {\theta _{0}}{2}}={\frac {1}{2}}\theta _{0}-{\frac {1}{48}}\theta _{0}^{3}+{\frac {1}{3\,840}}\theta _{0}^{5}-{\frac {1}{645\,120}}\theta _{0}^{7}+\cdots .

is used in the Legendre polynomial solution above. The resulting power series is:^[1]

{\begin{alignedat}{2}T&=2\pi {\sqrt {\frac {\ell }{g}}}\left(1+{\frac {1}{16}}\theta _{0}^{2}+{\frac {11}{3\,072}}\theta _{0}^{4}+{\frac {173}{737\,280}}\theta _{0}^{6}+{\frac {22\,931}{1\,321\,205\,760}}\theta _{0}^{8}+{\frac {1\,319\,183}{951\,268\,147\,200}}\theta _{0}^{10}+{\frac {233\,526\,463}{2\,009\,078\,326\,886\,400}}\theta _{0}^{12}+\cdots \right)\end{alignedat}}.

Arithmetic-geometric mean solution for elliptic integral

Given Eq. 3 and the arithmetic–geometric mean solution of the elliptic integral:

K(k)={\frac {\frac {\pi }{2}}{M(1-k,1+k)}},

where $M (x, y)$ is the arithmetic-geometric mean of $x$ and $y$ .

This yields an alternative and faster-converging formula for the period:^[2]^[3]^[4]

T={\frac {2\pi }{M\left(1,\cos {\frac {\theta _{0}}{2}}\right)}}{\sqrt {\frac {\ell }{g}}}.

Examples

The animations below depict the motion of a simple (frictionless) pendulum with increasing amounts of initial displacement of the bob, or equivalently increasing initial velocity. The small graph above each pendulum is the corresponding phase plane diagram; the horizontal axis is displacement and the vertical axis is velocity. With a large enough initial velocity the pendulum does not oscillate back and forth but rotates completely around the pivot.

Initial angle of 0°, a stable equilibrium.
Initial angle of 45°
Initial angle of 90°
Initial angle of 135°
Initial angle of 170°
Initial angle of 180°, unstable equilibrium.
Pendulum with just barely enough energy for a full swing
Pendulum with enough energy for a full swing

Compound pendulum

A compound pendulum (or physical pendulum) is one where the rod is not massless, and may have extended size; that is, an arbitrarily shaped rigid body swinging by a pivot. In this case the pendulum's period depends on its moment of inertia $I$ around the pivot point.

The equation of torque gives:

\tau = I \alpha\,

where:

α

is the angular acceleration.

τ

is the torque

The torque is generated by gravity so:

\tau = - m g L \sin\theta\,

where:

m

is the mass of the body

L

is the distance from the pivot to the center of mass of the pendulum

θ

is the angle from the vertical

Hence, under the small-angle approximation $sin θ \approx θ$ ,

\alpha =\theta ''\approx -{\frac {mgL\theta }{I_{\mathrm {cm} }+mL^{2}}}

where $I cm$ is the moment of inertia of the body about its center of mass.

The expression for $α$ is of the same form as the conventional simple pendulum and gives a period of^[5]

T=2\pi {\sqrt {\frac {I_{\mathrm {cm} }+mL^{2}}{mgL}}}

And a frequency of

f={\frac {1}{T}}={\frac {1}{2\pi }}{\sqrt {\frac {mgL}{I_{\mathrm {cm} }+mL^{2}}}}

If the initial angle is taken into consideration (for large amplitudes), then the expression for $\alpha$ becomes:

\alpha =\theta ''=-{\frac {mgL\sin \theta }{I_{\mathrm {cm} }+mL^{2}}}

and gives a period of:

T=4K\left(\sin ^{2}{\frac {\theta _{0}}{2}}\right){\sqrt {\frac {I_{\mathrm {cm} }+mL^{2}}{mgL}}}

where $θ 0$ is the maximum angle of oscillation (with respect to the vertical) and $K (k)$ is the complete elliptic integral of the first kind.

Physical interpretation of the imaginary period

The Jacobian elliptic function that expresses the position of a pendulum as a function of time is a doubly periodic function with a real period and an imaginary period. The real period is of course the time it takes the pendulum to go through one full cycle. Paul Appell pointed out a physical interpretation of the imaginary period:^[6] if $θ 0$ is the maximum angle of one pendulum and $180° - θ 0$ is the maximum angle of another, then the real period of each is the magnitude of the imaginary period of the other. This interpretation, involving dual forces in opposite directions, might be further clarified and generalized to other classical problems in mechanics with dual solutions.^[7]

References

↑ Nelson, Robert; M. G. Olsson (February 1986). "The pendulum — Rich physics from a simple system". American Journal of Physics. 54 (2): 112–121. doi:10.1119/1.14703. Retrieved 2012-04-30.
↑ Carvalhaes, Claudio G.; Suppes, Patrick (December 2008), "Approximations for the period of the simple pendulum based on the arithmetic-geometric mean" (PDF), Am. J. Phys., 76 (12͒): 1150–1154, doi:10.1119/1.2968864͔, ISSN 0002-9505, retrieved 2013-12-14
↑ Borwein, J.M.; Borwein, P.B. (1987). Pi and the AGM. New York: Wiley. pp. 1–15. ISBN 0-471-83138-7. MR 0877728.
↑ Van Baak, Tom (November 2013). "A New and Wonderful Pendulum Period Equation" (PDF). Horological Science Newsletter. 2013 (5): 22–30.
↑ Physical Pendulum
↑ Appell, Paul (July 1878). "Sur une interprétation des valeurs imaginaires du temps en Mécanique" [On an interpretation of imaginary time values in mechnics]. Comptes Rendus Hebdomadaires des Scéances de l'Académie des Sciences. 87 (1).
↑ Adlaj, S. (2012), "Mechanical interpretation of negative and imaginary tension of a tether in a linear parallel force field", Selected papers of the International Scientific Conference on Mechanics "Sixth Polyakhov Readings", Saint Petersburg, p. 13–18

External links

This article is issued from Wikipedia - version of the 11/1/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.