Equation of time

The equation of time describes the discrepancy between two kinds of solar time. The word equation is used in the medieval sense of reconcile a difference. The two times that differ are the apparent solar time, which directly tracks the motion of the sun, and mean solar time, which tracks a theoretical "mean" sun with noons 24 hours apart. Apparent (or true) solar time can be obtained by measurement of the current position (hour angle) of the Sun, as indicated (with limited accuracy) by a sundial. Mean solar time, for the same place, would be the time indicated by a steady clock set so that over the year its differences from apparent solar time would resolve to zero.[1]
The equation of time is the east or west component of the analemma, a curve representing the angular offset of the Sun from its mean position on the celestial sphere as viewed from Earth. The equation of time values for each day of the year, compiled by astronomical observatories, were widely listed in almanacs and ephemerides.[2][3]
The concept
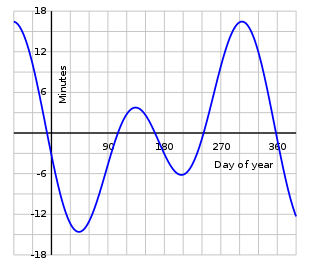
During a year the equation of time varies as shown on the graph; its change from one year to the next is slight. Apparent time, and the sundial, can be ahead (fast) by as much as 16 min 33 s (around 3 November), or behind (slow) by as much as 14 min 6 s (around 12 February). The equation of time has zeros near 15 April, 13 June, 1 September and 25 December. Ignoring very slow changes in the Earth's orbit and rotation, these events are repeated at the same times every tropical year. However, due to the non-integer number of days in a year, these dates can vary by a day or so from year to year.[4][5]
The graph of the equation of time is closely approximated by the sum of two sine curves, one with a period of a year and one with a period of half a year. The curves reflect two astronomical effects, each causing a different non-uniformity in the apparent daily motion of the Sun relative to the stars:
- the obliquity of the ecliptic (the plane of the Earth's annual orbital motion around the Sun), which is inclined by about 23.44 degrees relative to the plane of the Earth's equator; and
- the eccentricity of the Earth's orbit around the Sun, which is about 0.0167.
The equation of time is constant only for a planet with zero axial tilt and zero orbital eccentricity. On Mars the difference between sundial time and clock time can be as much as 50 minutes, due to the considerably greater eccentricity of its orbit. The planet Uranus, which has an extremely large axial tilt, has an equation of time that makes its days start and finish several hours earlier or later depending on the time of its solar year orbital period.
Sign of the equation of time
There is no universally accepted definition of the sign of the equation of time. Some publications show it as positive when a sundial is ahead of a clock, as shown in the upper graph above; others when the clock is ahead of the sundial, as shown in the lower graph. In the English-speaking world, the former usage is the more common, but is not always followed. Anyone who makes use of a published table or graph should first check its sign usage. Often, there is a note or caption which explains it. Otherwise, the sign can be determined by knowing that, during the first three months of each year, the clock is ahead of the sundial. The mnemonic "NYSS" (pronounced "nice"), for "new year, sundial slow", can be useful. Some published tables avoid the ambiguity by not using signs, but by showing phrases such as "sundial fast" or "sundial slow" instead.[6]
In this article, and others in English Wikipedia, a positive value of the equation of time implies that a sundial is ahead of a clock.
History
The phrase "equation of time" is derived from the medieval Latin, aequātiō diērum meaning "equation of days" or "difference of days". The word aequātiō was widely used in early astronomy to tabulate the difference between an observed value and the expected value (as in the equation of centre, the equation of the equinoxes, the equation of the epicycle). The difference between apparent solar time and mean time was recognized by astronomers since antiquity, but prior to the invention of accurate mechanical clocks in the mid-17th century, sundials were the only reliable timepieces, and solar time was the generally accepted standard.
A description of apparent and mean time was given by Nevil Maskelyne in the Nautical Almanac for 1767: "Apparent Time is that deduced immediately from the Sun, whether from the Observation of his passing the Meridian, or from his observed Rising or Setting. This Time is different from that shewn by Clocks and Watches well regulated at Land, which is called equated or mean Time." (He went on to say that, at sea, the apparent time found from observation of the Sun must be corrected by the equation of time, if the observer requires the mean time.)[1]
The right time was essentially defined as that which was shown by a sundial. When good mechanical clocks were introduced, they agreed with sundials only near four dates each year, so the equation of time was used to "correct" their readings to obtain sundial time. Some clocks, called equation clocks, included an internal mechanism to perform this "correction". Later, as clocks became the dominant good timepieces, uncorrected clock time, i.e., "mean time" became the accepted standard. The readings of sundials, when they were used, were then, and often still are, corrected with the equation of time, used in the reverse direction from previously, to obtain clock time. Many sundials, therefore, have tables or graphs of the equation of time engraved on them to allow the user to make this correction.
The equation of time was used historically to set clocks. Between the invention of accurate clocks in 1656 and the advent of commercial time distribution services around 1900, there were three common land-based ways to set clocks. Firstly, in the unusual event of having an astronomer present, the sun's transit across the meridian (the moment the sun passed overhead) was noted, the clock was then set to noon and offset by the number of minutes given by the equation of time for that date. Secondly, and much more commonly, a sundial was read, a table of the equation of time (usually engraved on the dial), was consulted and the watch or clock set accordingly. These calculated the mean time, albeit local to a point of longitude. (The third method did not use the equation of time; instead, it used stellar observations to give sidereal time, exploiting the relationship between sidereal time and solar time.)[7]
Of course, the equation of time can still be used, when required, to obtain solar time from clock time. Devices such as solar trackers, which move to keep pace with the Sun's movements in the sky, frequently do not include sensors to determine the Sun's position. Instead, they are controlled by a clock mechanism, along with a mechanism that incorporates the equation of time to make the device keep pace with the Sun.
Ancient history — Babylon and Egypt
The irregular daily movement of the Sun was known by the Babylonians. Book III of Ptolemy's Almagest is primarily concerned with the Sun's anomaly, and he tabulated the equation of time in his Handy Tables.[8] Ptolemy discusses the correction needed to convert the meridian crossing of the Sun to mean solar time and takes into consideration the nonuniform motion of the Sun along the ecliptic and the meridian correction for the Sun's ecliptic longitude. He states the maximum correction is 8 1⁄3 time-degrees or 5⁄9 of an hour (Book III, chapter 9).[9] However he did not consider the effect to be relevant for most calculations since it was negligible for the slow-moving luminaries and only applied it for the fastest-moving luminary, the Moon.
Medieval and Renaissance astronomy
Based on Ptolemy's discussion in the Almagest, medieval Islamic astronomers such as al-Khwarizmi, al-Battani, Kushyar ibn Labban, Jamshīd al-Kāshī and others, made improvements to the solar tables and the value of obliquity, and published tables of the equation of time (taʿdīl al-ayyām bi layālayhā) in their zij (astronomical tables).[10]
After that, the next substantial improvement in the computation didn't come until Kepler's final upset of the geocentric astronomy of the ancients. Gerald J. Toomer uses the medieval term "equation" from the Latin aequātiō[n 1], for Ptolemy's difference between the mean solar time and the true solar time. Johannes Kepler's definition of the equation is "the difference between the number of degrees and minutes of the mean anomaly and the degrees and minutes of the corrected anomaly."[11]
Apparent time versus mean time
Until the invention of the pendulum and the development of reliable clocks during the 17th century, the equation of time as defined by Ptolemy remained a curiosity, of importance only to astronomers. However, when mechanical clocks started to take over timekeeping from sundials, which had served humanity for centuries, the difference between clock time and solar time became an issue for everyday life. Apparent solar time (or true or real solar time) is the time indicated by the Sun on a sundial (or measured by its transit over a preferred local meridian), while mean solar time is the average as indicated by well-regulated clocks. The first tables to give the equation of time in an essentially correct way were published in 1665 by Christiaan Huygens.[12] Huygens, following the tradition of Ptolemy and medieval astronomers in general, set his values for the equation of time so as to make all values positive throughout the year.[13][n 2]
Another set of tables was published in 1672–73 by John Flamsteed, who later became the first Astronomer Royal of the new Royal Greenwich Observatory. These appear to have been the first essentially correct tables that gave today's meaning of Mean Time (rather than mean time based on the latest sunrise of the year as proposed by Huygens). Flamsteed adopted the convention of tabulating and naming the correction in the sense that it was to be applied to the apparent time to give mean time.[14]
The equation of time, correctly based on the two major components of the Sun's irregularity of apparent motion,[n 3] was not generally adopted until after Flamsteed's tables of 1672–73, published with the posthumous edition of the works of Jeremiah Horrocks.[15]
Robert Hooke (1635–1703), who mathematically analyzed the universal joint, was the first to note that the geometry and mathematical description of the (non-secular) equation of time and the universal joint were identical, and proposed the use of a universal joint in the construction of a "mechanical sundial".[16]
18th and early 19th centuries
The corrections in Flamsteed's tables of 1672–1673 and 1680 gave mean time computed essentially correctly and without need for further offset. But the numerical values in tables of the equation of time have somewhat changed since then, owing to three factors:
- general improvements in accuracy that came from refinements in astronomical measurement techniques,
- slow intrinsic changes in the equation of time, occurring as a result of small long-term changes in the Earth's obliquity and eccentricity (affecting, for instance, the distance and dates of perihelion), and
- the inclusion of small sources of additional variation in the apparent motion of the Sun, unknown in the 17th century, but discovered from the 18th century onwards, including the effects of the Moon[n 4], Venus and Jupiter.[17]
From 1767 to 1833, the British Nautical Almanac and Astronomical Ephemeris tabulated the equation of time in the sense 'mean minus apparent solar time'. Times in the Almanac were in apparent solar time, because time aboard ship was most often determined by observing the Sun. In the unusual case that the mean solar time of an observation was needed, one would apply the equation of time to apparent solar time. In the issues since 1834, all times have been in mean solar time, because by then the time aboard ship was increasingly often determined by marine chronometers. In the unusual case that the apparent solar time of an observation was needed, one would apply the equation of time to mean solar time, requiring all differences in the equation of time to have the opposite sign than before.
As the apparent daily movement of the Sun is one revolution per day, that is 360° every 24 hours, and the Sun itself appears as a disc of about 0.5° in the sky, simple sundials can be read to a maximum accuracy of about one minute. Since the equation of time has a range of about 33 minutes, the difference between sundial time and clock time cannot be ignored. In addition to the equation of time, one also has to apply corrections due to one's distance from the local time zone meridian and summer time, if any.
The tiny increase of the mean solar day due to the slowing down of the Earth's rotation, by about 2 ms per day per century, which currently accumulates up to about 1 second every year, is not taken into account in traditional definitions of the equation of time, as it is imperceptible at the accuracy level of sundials.
Explanations for the major components of the equation of time
Eccentricity of the Earth's orbit

The Earth revolves around the Sun. As seen from Earth, the Sun appears to revolve once around the Earth through the background stars in one year. If the Earth orbited the Sun with a constant speed, in a circular orbit in a plane perpendicular to the Earth's axis, then the Sun would culminate every day at exactly the same time, and be a perfect time keeper (except for the very small effect of the slowing rotation of the Earth). But the orbit of the Earth is an ellipse not centered on the Sun, and its speed varies between 30.287 and 29.291 km/s, according to Kepler's laws of planetary motion, and its angular speed also varies, and thus the Sun appears to move faster (relative to the background stars) at perihelion (currently around 3 January) and slower at aphelion a half year later. At these extreme points this effect varies the real solar day by 7.9 s/day from its mean. Consequently, the smaller daily differences on other days in speed are cumulative until these points, reflecting how the planet accelerates and decelerates compared to the mean. As a result, the eccentricity of the Earth's orbit contributes a sine wave variation with an amplitude of 7.66 min and a period of one year to the equation of time. The zero points are reached at perihelion (at the beginning of January) and aphelion (beginning of July); the extreme values are in early April (negative) and early October (positive).
Obliquity of the ecliptic

However, even if the Earth's orbit were circular, the perceived motion of the Sun along our celestial equator would still not be uniform. This is a consequence of the tilt of the Earth's rotational axis with respect to the plane of its orbit, or equivalently, the tilt of the ecliptic (the path of the Sun seems to take in the celestial sphere) with respect to the celestial equator. The projection of this motion onto our celestial equator, along which "clock time" is measured, is a maximum at the solstices, when the yearly movement of the Sun is parallel to the equator (causing amplification of perceived speed) and yields mainly a change in right ascension. It is a minimum at the equinoxes, when the Sun's apparent motion is more sloped and yields more change in declination, leaving less for the component in right ascension, which is the only component that affects the duration of the solar day. A practical illustration of obliquity is that the daily shift of the shadow cast by the Sun in a sundial even on the equator is smaller close to the equinoxes and greater close to the solstices. If this effect operated alone, then days would be up to 24 hours and 20.3 seconds long (measured solar noon to solar noon) near the solstices, and as much as 20.3 seconds shorter than 24 hours near the equinoxes.
In the figure on the right, we can see the monthly variation of the apparent slope of the plane of the ecliptic at solar midday as seen from Earth. This variation is due to the apparent precession of the rotating Earth through the year, as seen from the Sun at solar midday.
In terms of the equation of time, the inclination of the ecliptic results in the contribution of a sine wave variation with an amplitude of 9.87 minutes and a period of a half year to the equation of time. The zero points of this sine wave are reached at the equinoxes and solstices, while the extrema are at the beginning of February and August (negative) and the beginning of May and November (positive).
Secular effects
The two above mentioned factors have different wavelengths, amplitudes and phases, so their combined contribution is an irregular wave. At epoch 2000 these are the values (in minutes and seconds with UT dates):
| Point | Value | Date |
|---|---|---|
| minimum | −14 min 15 s | 11 February |
| zero | 0 min 0 s | 15 April |
| maximum | +3 min 41 s | 14 May |
| zero | 0 min 0 s | 13 June |
| minimum | −6 min 30 s | 26 July |
| zero | 0 min 0 s | 1 September |
| maximum | +16 min 25 s | 3 November |
| zero | 0 min 0 s | 25 December |
- E.T. = apparent − mean. Positive means: Sun runs fast and culminates earlier, or the sundial is ahead of mean time. A slight yearly variation occurs due to presence of leap years, resetting itself every 4 years.
The exact shape of the equation of time curve and the associated analemma slowly change[18] over the centuries, due to secular variations in both eccentricity and obliquity. At this moment both are slowly decreasing, but they increase and decrease over a timescale of hundreds of thousands of years. If and when the Earth's orbital eccentricity (now about 0.0167 and slowly decreasing) reaches 0.047, the eccentricity effect may in some circumstances overshadow the obliquity effect, leaving the equation of time curve with only one maximum and minimum per year, as is the case on Mars.[19]
On shorter timescales (thousands of years) the shifts in the dates of equinox and perihelion will be more important. The former is caused by precession, and shifts the equinox backwards compared to the stars. But it can be ignored in the current discussion as our Gregorian calendar is constructed in such a way as to keep the vernal equinox date at 21 March (at least at sufficient accuracy for our aim here). The shift of the perihelion is forwards, about 1.7 days every century. In 1246 the perihelion occurred on 22 December, the day of the solstice, so the two contributing waves had common zero points and the equation of time curve was symmetrical: in Astronomical Algorithms Meeus gives February and November extrema of 15 m 39 s and May and July ones of 4 m 58 s. Before that time the February minimum was larger than the November maximum, and the May maximum larger than the July minimum. In fact, in years before −1900 (1901 BCE) the May maximum was larger than the November maximum. In the year −2000 (2001 BCE) the May maximum was +12 minutes and a couple seconds while the November maximum was just less than 10 minutes. The secular change is evident when one compares a current graph of the equation of time (see below) with one from 2000 years ago, e.g., one constructed from the data of Ptolemy.
Graphical representation

Practical use
If the gnomon (the shadow-casting object) is not an edge but a point (e.g., a hole in a plate), the shadow (or spot of light) will trace out a curve during the course of a day. If the shadow is cast on a plane surface, this curve will be a conic section (usually a hyperbola), since the circle of the Sun's motion together with the gnomon point define a cone. At the spring and fall equinoxes, the cone degenerates into a plane and the hyperbola into a line. With a different hyperbola for each day, hour marks can be put on each hyperbola which include any necessary corrections. Unfortunately, each hyperbola corresponds to two different days, one in each half of the year, and these two days will require different corrections. A convenient compromise is to draw the line for the "mean time" and add a curve showing the exact position of the shadow points at noon during the course of the year. This curve will take the form of a figure eight and is known as an analemma. By comparing the analemma to the mean noon line, the amount of correction to be applied generally on that day can be determined.
The equation of time is used not only in connection with sundials and similar devices, but also for many applications of solar energy. Machines such as solar trackers and heliostats have to move in ways that are influenced by the equation of time.
Civil time is the local mean time for a meridian that often passes near the center of the time zone, and may possibly be further altered by daylight saving time. When the apparent solar time that corresponds to a given civil time is to be found, the difference in longitude between the site of interest and the time zone meridian, daylight saving time, and the equation of time must all be considered.[20]
Calculating the equation of time
The equation of time is obtained from a published table, or a graph. For dates in the past such tables are produced from measurements done at the time, or by calculation; for future dates, of course, tables can only be calculated. In devices such as computer-controlled heliostats the computer is often programmed to calculate the equation of time. The calculation can be numerical or analytical. The former are based on numerical integration of the differential equations of motion, including all significant gravitational and relativistic effects. The results are accurate to better than 1 second and are the basis for modern almanac data. The latter are based on a solution that includes only the gravitational interaction between the Sun and Earth, simpler than but not as accurate as the former. Its accuracy can be improved by including small corrections.
The following discussion describes a reasonably accurate (agreeing with Almanac data to within 3 seconds over a wide range of years) algorithm for the equation of time that is well known to astronomers.[21] It also shows how to obtain a simple approximate formula (accurate to within 1 minute over a large time interval), that can be easily evaluated with a calculator and provides the simple explanation of the phenomenon that was used previously in this article.
Mathematical description
The precise definition of the equation of time is[22]
- EOT = GHA − GMHA
The quantities occurring in this equation are
- EOT, the time difference between apparent solar time and mean solar time;
- GHA, the Greenwich Hour Angle of the apparent (actual) Sun;
- GMHA = Universal Time − Offset, the Greenwich Mean Hour Angle of the mean (fictitious) Sun.
Here time and angle are quantities that are related by factors such as: 2π radians = 360° = 1 day = 24 hours. The difference, EOT, is measurable since GHA is an angle that can be measured and Universal Time, UT, is a scale for the measurement of time. The offset by π = 180° = 12 hours from UT is needed because UT is zero at mean midnight while GMHA = 0 at mean noon.[n 5] Both GHA and GMHA, like all physical angles, have a mathematical, but not a physical discontinuity at their respective (apparent and mean) noon. Despite the mathematical discontinuities of its components, EOT is defined as a continuous function by adding (or subtracting) 24 hours in the small time interval between the discontinuities in GHA and GMHA.
According to the definitions of the angles on the celestial sphere GHA = GAST − α (see hour angle)
where:
- GAST is the Greenwich apparent sidereal time (the angle between the apparent vernal equinox and the meridian in the plane of the equator). This is a known function of UT.[23]
- α is the right ascension of the apparent Sun (the angle between the apparent vernal equinox and the actual Sun in the plane of the equator).
On substituting into the equation of time, it is
- EOT = GAST − α − UT + offset
Like the formula for GHA above, one can write GMHA = GAST − αM, where the last term is the right ascension of the mean Sun. The equation is often written in these terms as[24]
- EOT = αM − α
where αM = GAST − UT + offset. In this formulation a measurement or calculation of EOT at a certain value of time depends on a measurement or calculation of α at that time. Both α and αM vary from 0 to 24 hours during the course of a year. The former has a discontinuity at a time that depends on the value of UT, while the later has its at a slightly later time. As a consequence, when calculated this way EOT has two, artificial, discontinuities. They can both be removed by subtracting 24 hours from the value of EOT in the small time interval after the discontinuity in α and before the one in αM. The resulting EOT is a continuous function of time.
Another definition, denoted E to distinguish it from EOT, is
- E = GMST − α − UT + offset
Here GMST = GAST − eqeq, is the Greenwich mean sidereal time (the angle between the mean vernal equinox and the mean Sun in the plane of the equator). Therefore, GMST is an approximation to GAST (and E is an approximation to EOT); eqeq is called the equation of the equinoxes and is due to the wobbling, or nutation of the Earth's axis of rotation about its precessional motion. Since the amplitude of the nutational motion is only about 1.2 s (18″ of longitude) the difference between EOT and E can be ignored unless one is interested in subsecond accuracy.
A third definition, denoted Δt to distinguish it from EOT and E, and now called the Equation of Ephemeris Time[25] (prior to the distinction that is now made between EOT, E, and Δt the latter was known as the equation of time) is
- Δt = Λ − α
here Λ is the ecliptic longitude of the mean Sun (the angle from the mean vernal equinox to the mean Sun in the plane of the ecliptic).
The difference Λ − (GMST − UT + offset) is 1.3 s from 1960 to 2040. Therefore, over this restricted range of years Δt is an approximation to EOT whose error is in the range 0.1 to 2.5 s depending on the longitude correction in the equation of the equinoxes; for many purposes, for example correcting a sundial, this accuracy is more than good enough.
Right ascension calculation
The right ascension, and hence the equation of time, can be calculated from Newton's two-body theory of celestial motion, in which the bodies (Earth and Sun) describe elliptical orbits about their common mass center. Using this theory, the equation of time becomes
- Δt = M + λp − α
where the new angles that appear are
- M = 2π(t − tp)/tY, is the mean anomaly, the angle from the periapsis of the elliptical orbit to the mean Sun; its range is from 0 to 2π as t increases from tp to tp + tY;
- tY = 365.2596358 days is the length of time in an anomalistic year: the time interval between two successive passages of the periapsis;
- λp = Λ − M, is the ecliptic longitude of the periapsis;
- t is dynamical time, the independent variable in the theory. Here it is taken to be identical with the continuous time based on UT (see above), but in more precise calculations (of E or EOT) the small difference between them must be accounted for[26] as well as the distinction between UT1 and UTC.
To complete the calculation three additional angles are required:
- E, the Sun's eccentric anomaly (note that this is different from M);
- ν, the Sun's true anomaly;
- λ = ν + λp, the Sun's true longitude on the ecliptic.

All these angles are shown in the figure on the right, which shows the celestial sphere and the Sun's elliptical orbit seen from the Earth (the same as the Earth's orbit seen from the Sun). In this figure ε is the obliquity, while e = √1 − (b/a)2 is the eccentricity of the ellipse.
Now given a value of 0 ≤ M ≤ 2π, one can calculate α(M) by means of the following well-known procedure:[21]
First, given M, calculate E from Kepler's equation:[27]
- M = E − e sin E
Although this equation cannot be solved exactly in closed form, values of E(M) can be obtained from infinite (power or trigonometric) series, graphical, or numerical methods. Alternatively, note that for e = 0, E = M, and by iteration:[28]
- E ≈ M + e sin M.
This approximation can be improved, for small e, by iterating again,
- E ≈ M + e sin M + 1/2e2 sin 2M,
and continued iteration produces successively higher order terms of the power series expansion in e. For small values of e (much less than 1) two or three terms of the series give a good approximation for E; the smaller e, the better the approximation.
Next, knowing E, calculate the true anomaly ν from an elliptical orbit relation[29]
The correct branch of the multiple valued function tan−1 x to use is the one that makes ν a continuous function of E(M) starting from νE=0 = 0. Thus for 0 ≤ E < π use tan−1 x = Tan−1 x, and for π < E ≤ 2π use tan−1 x = Tan−1 x + π. At the specific value E = π for which the argument of tan is infinite, use ν = E. Here Tan−1 x is the principal branch, | Tan−1 x | < π/2; the function that is returned by calculators and computer applications. Alternatively, this function can be expressed in terms of its Taylor series in e, the first three terms of which are:
- ν ≈ E + e sin E + 1/4e2 sin 2E.
For small e this approximation (or even just the first two terms) is a good one. Combining the approximation for E(M) with this one for ν(E) produces
- ν ≈ M + 2e sin M + 5/4e2 sin 2M.
The relation ν(M) is called the equation of the center; the expression written here is a second-order approximation in e. For the small value of e that characterises the Earth's orbit this gives a very good approximation for ν(M).
Next, knowing ν, calculate λ from its definition:
- λ = ν + λp
The value of λ varies non-linearly with M because the orbit is elliptical and not circular. From the approximation for ν:
- λ ≈ M + λp + 2e sin M + 5/4e2 sin 2M.
Finally, knowing λ calculate α from a relation for the right triangle on the celestial sphere shown above[30]
- α = tan−1(cos ε tan λ)
Note that the quadrant of α is the same as that of λ, therefore reduce λ to the range 0 to 2π and write
- α = Tan−1 (cos ε tan λ) + kπ,
where k is 0 if λ is in quadrant 1, it is 1 if λ is in quadrants 2 or 3 and it is 2 if λ is in quadrant 4. For the values at which tan is infinite, α = λ.
Although approximate values for α can be obtained from truncated Taylor series like those for ν,[31] it is more efficacious to use the equation[32]
- α = λ − sin−1 [y sin (α + λ)]
where y = tan2(ε/2). Note that for ε = y = 0, α = λ and iterating twice:
- α ≈ λ − y sin 2λ + 1/2y2 sin 4λ.
Equation of time
The equation of time is obtained by substituting the result of the right ascension calculation into an equation of time formula. Here Δt(M) = M + λp − α[λ(M)] is used; in part because small corrections (of the order of 1 second), that would justify using E, are not included, and in part because the goal is to obtain a simple analytical expression. Using two term approximations for λ(M) and α(λ), allows Δt to be written as an explicit expression of two terms, which is designated Δtey because it is a first order approximation in e and in y.
- Δtey = −2e sin M + y sin (2M + 2λp) = −7.659 sin M + 9.863 sin (2M + 3.5932) minutes
This equation was first derived by Milne,[33] who wrote it in terms of λ = M + λp. The numerical values written here result from using the orbital parameter values, e = 0.016709, ε = 23.4393° = 0.409093 radians, and λp = 282.9381° = 4.938201 radians that correspond to the epoch 1 January 2000 at 12 noon UT1. When evaluating the numerical expression for Δtey as given above, a calculator must be in radian mode to obtain correct values because the value of 2λp − 2π in the argument of the second term is written there in radians. Higher order approximations can also be written,[34] but they necessarily have more terms. For example, the second order approximation in both e and y consists of five terms[35]
- Δte2y2 = Δtey − 5/4e2 sin 2M + ey sin M cos (2M + 2λp) − 1/2y2 sin (4M + 4λp)
This approximation has the potential for high accuracy, however in order to achieve it over a wide range of years, the parameters e, ε, and λp must be allowed to vary with time.[36] This creates additional calculational complications. Other approximations have been proposed, for example, Δte[37] which uses the first order equation of the center but no other approximation to determine α, and Δte2[38] which uses the second order equation of the center.
The time variable, M, can be written either in terms of n, the number of days past perihelion, or D, the number of days past a specific date and time (epoch):
- M = 2π/tYn days = MD + 2π/tYD days = 6.24004077 + 0.01720197D
Here MD is the value of M at the chosen date and time. For the values given here, in radians, MD is that measured for the actual Sun at the epoch, 1 January 2000 at 12 noon UT1, and D is the number of days past that epoch. At periapsis M = 2π, so solving gives D = Dp = 2.508109. This puts the periapsis on 4 January 2000 at 00:11:41 while the actual periapsis is, according to results from the Multiyear Interactive Computer Almanac[39] (abbreviated as MICA), on 3 January 2000 at 05:17:30. This large discrepancy happens because the difference between the orbital radius at the two locations is only 1 part in a million; in other words, radius is a very weak function of time near periapsis. As a practical matter this means that one cannot get a highly accurate result for the equation of time by using n and adding the actual periapsis date for a given year. However, high accuracy can be achieved by using the formulation in terms of D.

When D > Dp, M is greater than 2π and one must subtract a multiple of 2π (that depends on the year) from it to bring it into the range 0 to 2π. Likewise for years prior to 2000 one must add multiples of 2π. For example, for the year 2010, D varies from 3653 on 1 January at noon to 4017 on 31 December at noon, the corresponding M values are 69.0789468 and 75.3404748 and are reduced to the range 0 to 2π by subtracting 10 and 11 times 2π respectively. One can always write D = nY + d, where nY is the number of days from the epoch to noon on 1 January of the desired year, and 0 ≤ d ≤ 364 (365 if the calculation is for a leap year).
The result of the computations is usually given as either a set of tabular values, or a graph of the equation of time as a function of d. A comparison of plots of Δt, Δtey, and results from MICA all for the year 2000 is shown in the figure on the right. The plot of Δtey is seen to be close to the results produced by MICA, the absolute error, Err = | Δtey − MICA2000 |, is less than 1 minute throughout the year; its largest value is 43.2 seconds and occurs on day 276 (3 October). The plot of Δt is indistinguishable from the results of MICA, the largest absolute error between the two is 2.46 s on day 324 (20 November).
Remark on the continuity of the equation of time
For the choice of the appropriate branch of the arctan relation with respect to function continuity a modified version of the arctangent function is helpful. It brings in previous knowledge about the expected value by a parameter. The modified arctangent function is defined as:
- arctanη x = arctan x + π round (η − x/π).
It produces a value that is as close to η as possible. The function round rounds to the nearest integer.
Applying this yields:
- Δt(M) = M + λp − arctan(M+λp) (cos ε tan λ).
The parameter M + λp arranges here to set Δt to the zero nearest value which is the desired one.
Secular effects
The difference between the MICA and Δt results was checked every 5 years over the range from 1960 to 2040. In every instance the maximum absolute error was less than 3 s; the largest difference, 2.91 s, occurred on 22 May 1965 (day 141). However, in order to achieve this level of accuracy over this range of years it is necessary to account for the secular change in the orbital parameters with time. The equations that describe this variation are:[40]
According to these relations, in 100 years (D = 36525), λp increases by about 0.5% (1.7°), e decreases by about 0.25%, and ε decreases by about 0.05%.
As a result, the number of calculations required for any of the higher-order approximations of the equation of time requires a computer to complete them, if one wants to achieve their inherent accuracy over a wide range of time. In this event it is no more difficult to evaluate Δt using a computer than any of its approximations.
In all this note that Δtey as written above is easy to evaluate, even with a calculator, is accurate enough (better than 1 minute over the 80-year range) for correcting sundials, and has the nice physical explanation as the sum of two terms, one due to obliquity and the other to eccentricity that was used previously in the article. This is not true either for Δt considered as a function of M or for any of its higher-order approximations.
Alternative calculation
Another calculation of the equation of time can be done as follows.[41] Angles are in degrees; the conventional order of operations applies.
- W = 360°/365.24 days
W is the Earth's mean angular orbital velocity in degrees per day.
- A = W × (D + 10)
D is the date, in days starting at zero on 1 January (i.e. the days part of the ordinal date minus 1). 10 is the approximate number of days from the December solstice to 1 January. A is the angle the earth would move on its orbit at its average speed from the December solstice to date D.
- B = A + 360°/π × 0.0167 × sin [W(D − 2)]
B is the angle the Earth moves from the solstice to date D, including a first-order correction for the Earth's orbital eccentricity, 0.0167. The number 2 is the number of days from 1 January to the date of the Earth's perihelion. This expression for B can be simplified by combining constants to:
- B = A + 1.914° × sin [W(D − 2)].
C is the difference between the angles moved at mean speed, and at the corrected speed projected onto the equatorial plane, and divided by 180 to get the difference in "half turns". The value 23.44° is the obliquity (tilt) of the Earth's axis. The subtraction gives the conventional sign to the equation of time. For any given value of x, arctan x (sometimes written as tan−1 x) has multiple values, differing from each other by integer numbers of half turns. The value generated by a calculator or computer may not be the appropriate one for this calculation. This may cause C to be wrong by an integer number of half turns. The excess half turns are removed in the next step of the calculation to give the equation of time:
- EOT = 720 × (C − nint(C)) minutes
The expression nint(C) means the nearest integer to C. On a computer, it can be programmed, for example, as INT(C + 0.5). It is 0, 1, or 2 at different times of the year. Subtracting it leaves a small positive or negative fractional number of half turns, which is multiplied by 720, the number of minutes (12 hours) that the Earth takes to rotate one half turn relative to the Sun, to get the equation of time.
Compared with published values,[6] this calculation has a root mean square error of only 3.7 s. The greatest error is 6.0 s. This is much more accurate than the approximation described above, but not as accurate as the elaborate calculation.
Computer code
The following code implements the "alternative calculation" as a function in Java. The day of the year is passed to the function as an integer value, using December 21 as Day 1 and it returns an equation of time value in seconds. It may be freely used and distributed, or re-written in another language.
/*
Equation of Time calculation
*** No guarantees are implied. Use at your own risk ***
Written by Del Smith, 2016-11-29
Based on "Equation of time" WikiPedia article as of 2016-11-28
(which describes angles in a bewildering mixture of degrees and radians)
It appears to give a good result, but I make no claims for accuracy.
*/
// constants (all angles as radians)
private static final Double pi = atan(1.0)*4; // tan(pi/4) = 1 (45 degrees)
private static final Double lambda = 23.44 * pi / 180; // Earth's inclination in radians
private static final Double omega = 2*pi/365.25; // angular velocity of annual revolution (radians/day)
// calculate the Equation of Time from 'day of year'
private static Double EqnOfTime(int day_number) {
// the result is in seconds
// add to the Mean Solar Time (UTC + Longitude*240 sec.) to get Apparent Solar Time
// D day of the year
// A = W*(D+10) angle of revolution (circular)
// B = A + 0.0333*sin(W*(D-2)) angle of revolution (elliptical)
// C = ( A - atan[ tan(B) / cos (inclination) ] ) / 'pi' angular correction
// EOT = 43200 × (C − int(C+0.5)) Equation of Time in seconds
Double delta = Integer.valueOf(day_number).doubleValue();
Double alpha = omega*((delta+10)%365); // angle in (mean) circular orbit, solar year starts 21. Dec
Double beta = alpha + 0.0333*sin(omega*((delta-2)%365)); // angle in elliptical orbit, from perigee 3. Jan (radians)
Double gamma = ( alpha - atan( tan(beta) / cos(lambda))) / pi; // angular correction
return (43200. * (gamma - Double.valueOf(gamma+0.5).intValue())); // equation of time in seconds
}
Addendum about solar declination
The value of B in the above calculation is an accurate value for the Sun's ecliptic longitude (shifted by 90°), so the solar declination becomes readily available:
- Declination = −arcsin (sin 23.44° × cos B)
which is accurate to within a fraction of a degree.
See also
Notes and Footnotes
- Notes
- ↑ (equalization [adjustment])
- ↑ This meant that any clock being set to mean time by Huygens's tables was consistently about 15 minutes slow compared to today's mean time.
- ↑ See above
- ↑ See barycentre
- ↑ Universal Time is discontinuous at mean midnight so another quantity day number N, an integer, is required in order to form the continuous quantity time t: t = N + UT/24 hr days.
- Footnotes
- 1 2 Nautical Almanac 1767
- ↑ Milham 1945, pp. 11–15
- ↑ See for example, British Commission on Longitude 1794, p. 14.
- ↑ As an example of the inexactness of the dates, according to the U.S. Naval Observatory's Multiyear Interactive Computer Almanac the equation of time was zero at 02:00 UT1 on 16 April 2011.
- ↑ Heilbron 1999, p. 277.
- 1 2 Waugh, p. 205
- ↑ Olmstead 1866, pp. 57–58
- ↑ Neugebauer, Otto (1975), A History of Ancient Mathematical Astronomy, New York / Heidelberg / Berlin: Springer-Verlag, pp. 984–986, ISBN 0-387-06995-X
- ↑ Toomer 1998, p. 171
- ↑ E.S. Kennedy, "A Survey of Islamic Astronomical Tables", Transactions of the American Philosophical Society, 46, Part 2 (1956), p. 19.
- ↑ Kepler 1995, p. 155
- ↑ Huygens, 1665
- ↑ Huygens 1665
- ↑ Flamsteed 1672
- ↑ Vince 1814, p. 49
- ↑ Mills 2007, p. 219
- ↑ Maskelyne 1764, pp. 163–169
- ↑ Karney, Kevin. "Variation in the Equation of Time" (PDF).
- ↑ Telling Time on Mars
- ↑ "How to find the exact time of solar noon" n.d.
- 1 2 Duffet-Smith p. 89
- ↑ Hughes et al., p.1529
- ↑ "Computing Greenwich Sidereal Time", Naval Oceanography Portal
- ↑ Heilbron p. 275, Roy p. 45
- ↑ Hughes, et. al., p. 1532
- ↑ Hughes, et. al., p. 1530, "Computing Greenwich Sidereal Time", Naval Oceanography Portal
- ↑ Moulton p. 159
- ↑ Hinch p. 2
- ↑ Moulton p. 165
- ↑ Burington p. 22
- ↑ Whitman p. 32
- ↑ Milne p. 374
- ↑ Milne p. 375
- ↑ Muller Eqs (45) and (46)
- ↑ Hughes, et. al., p1535
- ↑ Duffett-Smith, p. 86, Hughes, et. al., p. 1531,1535
- ↑ Duffett-Smith, p. 86, Williams
- ↑ "Approximate Solar Coordinates", Naval Oceanographic Portal
- ↑ U.S.Naval Observatory
- ↑ Duffett-Smith p. 86, Hughes, et. al., p. 1531,1535
- ↑ Williams
References
- "Approximate Solar Coordinates", "Naval Oceanography Portal".
- British Commission on Longitude (1794). Nautical Almanac and Astronomical Ephemeris for the year 1803. London, UK: C. Bucton.
- Burington R S 1949 Handbook of Mathematical Tables and Formulas (Sandusky, Ohio: Handbook Publishers)
- "Computing Greenwich Sidereal Time", "Naval Oceanography Portal".
- Duffett-Smith p. 1988 Practical Astronomy with your Calculator Third Edition (Cambridge: Cambridge University Press)
- Flamsteed, John (1673) [1672 for the imprint, and bound with other sections printed 1673]. De Inaequalitate Dierum Solarium. London: William Godbid.
- Heilbron J L 1999 The Sun in the Church, (Cambridge Mass: Harvard University Press ISBN 0-674-85433-0)
- Helyar, A.G. "Sun Data". Archived from the original on 11 January 2004.
- Hinch E J 1991 Perturbation Methods, (Cambridge: Cambridge University Press)
- "How to find the exact time of solar noon, wherever you are in the world." London: Spot-On Sundials. n.d. retrieved 23 July 2013.
- Hughes D W, et al. 1989, The Equation of Time, Monthly Notices of the Royal Astronomical Society 238 pp. 1529–1535
- Huygens, Christiaan (1665). Kort Onderwys aengaende het gebruyck der Horologien tot het vinden der Lenghten van Oost en West. The Hague: [publisher unknown].
- Kepler, Johannes (1995). Epitome of Copernican Astronomy & Harmonies of the World. Prometheus Books. ISBN 1-57392-036-3.
- Maskelyne, Nevil, "On the Equation of Time and the True Manner of Computing it", Philosophical Transactions, liv (1764), p. 336 (as reprinted in an abridged edition, 1809, vol.12, at p.163–169)
- Meeus, J 1997 Mathematical Astronomy Morsels, (Richmond, Virginia: Willman-Bell)
- Milham, Willis I. (1945). Time and Timekeepers. New York: MacMillan. ISBN 0780800087. pp. 11–15
- Milne R M 1921, "Note on the Equation of Time", The Mathematical Gazette 10 (The Mathematical Association) pp. 372–375.
- Mills, Allan (2007). "Robert Hooke's 'universal joint' and its application to sundials and the sundial-clock". Notes Rec. R. Soc. Royal Society Publishing. 61 (2): 219–236. doi:10.1098/rsnr.2006.0172. Retrieved 23 November 2011.
- Moulton F R 1970 An Introduction to Celestial Mechanics, Second Revised Edition, (New York: Dover).
- Muller M 1995, "Equation of Time – Problem in Astronomy", Acta Phys Pol A 88 Supplement, S-49.
- Olmstead, Dennison (1866). A Compendium of Astronomy. New York: Collins & Brother.
- Roy A E 1978 Orbital Motion, (Adam Hilger ISBN 0-85274-228-2)
- Toomer, G.J. (1998). Ptolemy's Almagest. Princeton University Press. p. 171. ISBN 0-691-00260-6.
- United States Naval Observatory April 2010, Multiyear Computer Interactive Almanac (version 2.2.1), Richmond VA: Willmann-Bell.
- Vince, S. "A Complete System of Astronomy". 2nd edition, volume 1, 1814.
- Waugh, Albert E. (1973). Sundials, Their Theory and Construction. New York: Dover Publications. p. 205. ISBN 0-486-22947-5.
- Whitman A M 2007, "A Simple Expression for the Equation of Time", Journal Of the North American Sundial Society 14 pp. 29–33.
- Williams, David O. (2009). "The Latitude and Longitude of the Sun". Archived from the original on 23 March 2012.
External links
| Wikimedia Commons has media related to Equation of time (sundials). |
- NOAA Solar Calculator
- USNO data services (include rise/set/transit times of the Sun and other celestial objects)
- The equation of time described on the Royal Greenwich Observatory Web site
- An analemma site with many illustrations
- The Equation of Time and the Analemma, by Kieron Taylor
- An article by Brian Tung containing a link to a C program using a more accurate formula than most (particularly at high inclinations and eccentricities). The program can calculate solar declination, Equation of Time, or Analemma.
- Doing calculations using Ptolemy's geocentric planetary models with a discussion of his E.T. graph
- Equation of Time Longcase Clock by John Topping C.1720
- The equation of time correction-table A page describing how to correct a clock to a sundial.
- Solar tempometer – Calculate your solar time, including the equation of time.