Axial tilt
In astronomy, axial tilt, also known as obliquity, is the angle between an object's rotational axis and its orbital axis, or, equivalently, the angle between its equatorial plane and orbital plane.[1] It differs from orbital inclination.
At an obliquity of zero, the two axes point in the same direction; i.e., the rotational axis is perpendicular to the orbital plane. Over the course of an orbit, the obliquity usually does not change considerably, and the orientation of the axis remains the same relative to the background stars. This causes one pole to be directed more toward the Sun on one side of the orbit, and the other pole on the other side — the cause of the seasons on the Earth. Earth's obliquity oscillates between 22.1 and 24.5 degrees on a 41,000-year cycle. It is currently 23°26′13.5″ (or 23.43709°) and decreasing.
Standards
| |
|
The positive pole of a planet is defined by the right-hand rule: if the fingers of the right hand are curled in the direction of the rotation then the thumb points to the positive pole. The axial tilt is defined as the angle between the direction of the positive pole and the normal to the orbital plane. The angles for Earth, Uranus and Venus are approximately 23°, 97°, and 177° respectively. |
There are two standard methods of specifying tilt. The International Astronomical Union (IAU) defines the north pole of a planet as that which lies on Earth's north side of the invariable plane of the Solar System;[2] under this system, Venus is tilted 3° and spins retrograde, opposite that of most of the other planets.[3][4]
The IAU also uses the right-hand rule to define a positive pole[5] for the purpose of determining orientation. Using this convention, Venus is tilted 177° ("upside down").
Earth
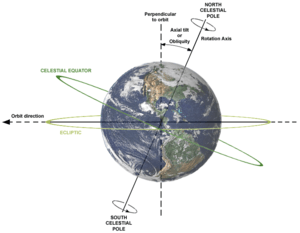
Earth's orbital plane is known as the ecliptic plane, and Earth's tilt is known to astronomers as the obliquity of the ecliptic, being the angle between the ecliptic and the celestial equator on the celestial sphere.[6] It is denoted by the Greek letter ε.
Earth currently has an axial tilt of about 23.4°.[7] This value remains approximately the same relative to a stationary orbital plane throughout the cycles of axial precession.[8] However, because the ecliptic (i.e., Earth's orbit) moves due to planetary perturbations, the obliquity of the ecliptic is not a fixed quantity. At present, it is decreasing at a rate of about 47″ per century (see details in Short term below).
History
Earth's obliquity may have been reasonably accurately measured as early as 1100 BC in India and China.[9] The ancient Greeks had good measurements of the obliquity since about 350 BC, when Pytheas of Marseilles measured the shadow of a gnomon at the summer solstice.[10] About 830 AD, the Caliph Al-Mamun of Baghdad directed his astronomers to measure the obliquity, and the result was used in the Arab world for many years.[11]
It was widely believed, during the Middle Ages, that both precession and Earth's obliquity oscillated around a mean value, with a period of 672 years, an idea known as trepidation of the equinoxes. Perhaps the first to realize this was incorrect (during historic time) was Ibn al-Shatir in the fourteenth century[12] and the first to realize that the obliquity is decreasing at a relatively constant rate was Fracastoro in 1538.[13] The first accurate, modern, western observations of the obliquity were probably those of Tycho Brahe from Denmark, about 1584,[14] although observations by several others, including al-Ma'mun, al-Tusi,[15] Purbach, Regiomontanus, and Walther, could have provided similar information.
Seasons
Earth's axis remains tilted in the same direction with reference to the background stars throughout a year (regardless of where it is in its orbit). This means that one pole (and the associated hemisphere of Earth) will be directed away from the Sun at one side of the orbit, and half an orbit later (half a year later) this pole will be directed towards the Sun. This is the cause of Earth's seasons. Summer occurs in the Northern hemisphere when the north pole is directed toward the Sun. Variations in Earth's axial tilt can influence the seasons and is likely a factor in long-term climate change (also see Milankovitch cycles).
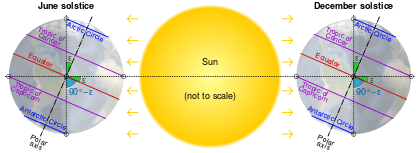
Oscillation
Short term
The exact angular value of the obliquity is found by observation of the motions of Earth and planets over many years. Astronomers produce new fundamental ephemerides as the accuracy of observation improves and as the understanding of the dynamics increases, and from these ephemerides various astronomical values, including the obliquity, are derived.
Annual almanacs are published listing the derived values and methods of use. Until 1983, the Astronomical Almanac's angular value of the obliquity for any date was calculated based on the work of Newcomb, who analyzed positions of the planets until about 1895:
- ε = 23° 27′ 8.26″ − 46.845″ T − 0.0059″ T2 + 0.00181″ T3
where ε is the obliquity and T is tropical centuries from B1900.0 to the date in question.[16]
From 1984, the Jet Propulsion Laboratory's DE series of computer-generated ephemerides took over as the fundamental ephemeris of the Astronomical Almanac. Obliquity based on DE200, which analyzed observations from 1911 to 1979, was calculated:
- ε = 23° 26′ 21.45″ − 46.815″ T − 0.0006″ T2 + 0.00181″ T3
where hereafter T is Julian centuries from J2000.0.[17]
JPL's fundamental ephemerides have been continually updated. For instance, the Astronomical Almanac for 2010 specifies:[7]
- ε = 23° 26′ 21.406″ − 46.836769″ T − 0.0001831″ T2 + 0.00200340″ T3 − 5.76″ × 10−7 T4 − 4.34″ × 10−8 T5
These expressions for the obliquity are intended for high precision over a relatively short time span, perhaps ± several centuries.[18] J. Laskar computed an expression to order T10 good to 0.02″ over 1000 years and several arcseconds over 10,000 years.
- ε = 23° 26′ 21.448″ − 4680.93″ t − 1.55″ t2 + 1999.25″ t3 − 51.38″ t4 − 249.67″ t5 − 39.05″ t6 + 7.12″ t7 + 27.87″ t8 + 5.79″ t9 + 2.45″ t10
where here t is multiples of 10,000 Julian years from J2000.0.[19]
These expressions are for the so-called mean obliquity, that is, the obliquity free from short-term variations. Periodic motions of the Moon and of Earth in its orbit cause much smaller (9.2 arcseconds) short-period (about 18.6 years) oscillations of the rotation axis of Earth, known as nutation, which add a periodic component to Earth's obliquity.[20][21] The true or instantaneous obliquity includes this nutation.[22]
Long term
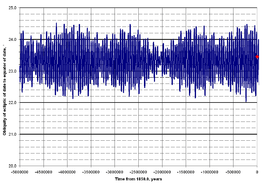
Using numerical methods to simulate Solar System behavior, long-term changes in Earth's orbit, and hence its obliquity, have been investigated over a period of several million years. For the past 5 million years, Earth's obliquity has varied between 22° 2′ 33″ and 24° 30′ 16″, with a mean period of 41,040 years. This cycle is a combination of precession and the largest term in the motion of the ecliptic. For the next 1 million years, the cycle will carry the obliquity between 22° 13′ 44″ and 24° 20′ 50″.[23]
The Moon has a stabilizing effect on Earth's obliquity. Frequency map analysis conducted in 1993 suggested that, in the absence of the Moon, the obliquity can change rapidly due to orbital resonances and chaotic behavior of the Solar System, reaching as high as 90° in as little as a few million years (also see Orbit of the Moon).[24][25] However, more recent numerical simulations[26] made in 2011 indicated that even in the absence of the Moon, Earth's obliquity might not be quite so unstable; varying only by about 20–25°. The Moon's stabilizing effect will continue for less than 2 billion years. If the Moon continues to recede from Earth due to tidal acceleration, resonances may occur which will cause large oscillations of the obliquity.[27]

Solar System bodies
All four of the innermost, rocky planets of the Solar System may have had large variations of their obliquity in the past. Like Earth, all of the rocky planets have a small precessional rotation of their spin axis. This rate varies due to, among other things, tidal dissipation and core-mantle interaction. When each planet reaches certain values of precession, orbital resonances may cause very large, chaotic changes in obliquity. Mercury and Venus have most likely been stabilized by the tidal dissipation of the Sun. Earth was stabilized by the Moon, as above, but before its capture, Earth, too, could have passed through times of instability. Mars's obliquity is currently in a chaotic state; it varies as much as 0° to 60° over some millions of years, depending on perturbations of the planets.[24][28] The obliquities of the outer planets are considered relatively stable. Some authors dispute that Mars's obliquity is chaotic, and show that tidal dissipation and viscous core-mantle coupling are adequate for it to have reached a fully damped state, similar to Mercury and Venus.[3][29]
| Body | NASA, J2000.0[30] | IAU, 0 Jan 2010, 0h TT[31] | ||||||
|---|---|---|---|---|---|---|---|---|
| Axial tilt (degrees) |
North Pole | Rotation (hours) |
Axial tilt (degrees) |
North Pole | Rotation (deg/day) | |||
| R.A. (degrees) | Dec. (degrees) | R.A. (degrees) | Dec. (degrees) | |||||
| Sun | 7.25 | 286.13 | 63.87 | 609.12B | 7.25A | 286.15 | 63.89 | 14.18 |
| Mercury | 0.03 | 281.01 | 61.42 | 1407.6 | 0.01 | 281.01 | 61.45 | 6.14 |
| Venus | 2.64 | 272.76 | 67.16 | –5832.6 | 2.64 | 272.76 | 67.16 | −1.48 |
| Earth | 23.44 | 0.00 | 90.00 | 23.93 | 23.4 | undef. | 90.00 | 360.99 |
| Moon | 6.68 | — | — | 655.73 | 1.54C | 270.00 | 66.54 | 13.18 |
| Mars | 25.19 | 317.68 | 52.89 | 24.62 | 25.19 | 317.67 | 52.88 | 350.89 |
| Jupiter | 3.13 | 268.05 | 64.49 | 9.93D | 3.12 | 268.06 | 64.50 | 870.54D |
| Saturn | 26.73 | 40.60 | 83.54 | 10.66D | 26.73 | 40.59 | 83.54 | 810.79D |
| Uranus | 82.23 | 257.43 | –15.10 | –17.24D | 82.23 | 257.31 | −15.18 | −501.16D |
| Neptune | 28.32 | 299.36 | 43.46 | 16.11D | 28.33 | 299.40 | 42.95 | 536.31D |
| PlutoE | 57.47 | (312.99) | (6.16) | –153.29 | 60.41 | 312.99 | 6.16 | −56.36 |
| A with respect to the ecliptic of 1850 B at 16° latitude; the Sun's rotation varies with latitude C with respect to the ecliptic; the Moon's orbit is inclined 5.16° to the ecliptic D from the origin of the radio emissions; the visible clouds generally rotate at different rate E NASA lists the coordinates of Pluto's positive pole; values in (parentheses) have been reinterpreted to correspond to the north/negative pole. | ||||||||
Extrasolar planets
The stellar obliquity ψs, i.e. the axial tilt of a star with respect to the orbital plane of one of its planets, has been determined for only a few systems. But for 49 stars as of today, the sky-projected spin-orbit misalignment λ has been observed,[32] which serves as a lower limit to ψs. Most of these measurements rely on the Rossiter–McLaughlin effect. So far, it has not been possible to constrain the obliquity of an extrasolar planet. But the rotational flattening of the planet and the entourage of moons and/or rings, which are traceable with high-precision photometry, e.g. by the space-based Kepler spacecraft, could provide access to ψp in the near future.
Astrophysicists have applied tidal theories to predict the obliquity of extrasolar planets. It has been shown that the obliquities of exoplanets in the habitable zone around low-mass stars tend to be eroded in less than 109 years,[33][34] which means that they would not have seasons as Earth has.
See also
References
- ↑ U.S. Naval Observatory Nautical Almanac Office (1992). P. Kenneth Seidelmann, ed. Explanatory Supplement to the Astronomical Almanac. University Science Books. p. 733. ISBN 0-935702-68-7.
- ↑ Explanatory Supplement 1992, p. 384
- 1 2 Correia, Alexandre C. M.; Laskar, Jacques; de Surgy, Olivier Néron (May 2003). "Long-term evolution of the spin of Venus I. theory" (PDF). Icarus. 163 (1): 1–23. Bibcode:2003Icar..163....1C. doi:10.1016/S0019-1035(03)00042-3.
- ↑ Correia, A. C. M.; Laskar, J. (2003). "Long-term evolution of the spin of Venus: II. numerical simulations" (PDF). Icarus. 163 (1): 24–45. Bibcode:2003Icar..163...24C. doi:10.1016/S0019-1035(03)00043-5.
- ↑ "Report of the IAU/IAG Working Group on cartographic coordinates and rotational elements: 2006". springer.com. Retrieved 26 February 2016.
- ↑ U.S. Naval Observatory Nautical Almanac Office; U.K. Hydrographic Office; H.M. Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. US Government Printing Office. p. M11. ISBN 978-0-7077-4082-9.
- 1 2 Astronomical Almanac 2010, p. B52
- ↑ Chauvenet, William (1906). A Manual of Spherical and Practical Astronomy. 1. J. B. Lippincott. pp. 604–605.
- ↑ Wittmann, A. (1979). "The Obliquity of the Ecliptic". Astronomy and Astrophysics. 73: 129–131. Bibcode:1979A&A....73..129W.
- ↑ Gore, J. E. (1907). Astronomical Essays Historical and Descriptive. p. 61.
- ↑ Marmery, J. V. (1895). Progress of Science. p. 33.
- ↑ Saliba, George (1994). A History of Arabic Astronomy: Planetary Theories During the Golden Age of Islam. p. 235.
- ↑ Dreyer, J. L. E. (1890). Tycho Brahe. p. 355.
- ↑ Dreyer (1890), p. 123
- ↑ Sayili, Aydin (1981). The Observatory in Islam. p. 78.
- ↑ U.S. Naval Observatory Nautical Almanac Office; H.M. Nautical Almanac Office (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office. Section 2B.
- ↑ U.S. Naval Observatory; H.M. Nautical Almanac Office (1989). The Astronomical Almanac for the Year 1990. US Government Printing Office. p. B18. ISBN 0-11-886934-5.
- ↑ Newcomb, Simon (1906). A Compendium of Spherical Astronomy. MacMillan. pp. 226–227.
- ↑ See table 8 and eq. 35 in Laskar, J. (1986). "Secular Terms of Classical Planetary Theories Using the Results of General Relativity". Astronomy and Astrophysics. 157: 59–70. Bibcode:1986A&A...157...59L. and erratum to article Laskar, J. (1986). "Errratum: Secular terms of classical planetary theories using the results of general theory". Astronomy and Astrophysics. 164: 437. Bibcode:1986A&A...164..437L. Units in article are arcseconds, which may be more convenient.
- ↑ Explanatory Supplement (1961), sec. 2C
- ↑ "Basics of Space Flight, Chapter 2". Jet Propulsion Laboratory/NASA. 2013-10-29. Retrieved 2015-03-26.
- ↑ Meeus, Jean (1991). "Chapter 21". Astronomical Algorithms. Willmann-Bell. ISBN 0-943396-35-2.
- ↑ Berger, A.L. (1976). "Obliquity and Precession for the Last 5000000 Years". Astronomy and Astrophysics. 51: 127–135. Bibcode:1976A&A....51..127B.
- 1 2 Laskar, J.; Robutel, P. (1993). "The Chaotic Obliquity of the Planets" (PDF). Nature. 361 (6413): 608–612. Bibcode:1993Natur.361..608L. doi:10.1038/361608a0. Archived from the original (PDF) on 2012-11-23.
- ↑ Laskar, J.; Joutel, F.; Robutel, P. (1993). "Stabilization of the Earth's Obliquity by the Moon" (PDF). Nature. 361 (6413): 615–617. Bibcode:1993Natur.361..615L. doi:10.1038/361615a0.
- ↑ Lissauer, J.J.; Barnes, J.W.; Chambers, J.E. (2011). "Obliquity variations of a moonless Earth" (PDF). Icarus. 217: 77–87. Bibcode:2012Icar..217...77L. doi:10.1016/j.icarus.2011.10.013.
- ↑ Ward, W.R. (1982). "Comments on the Long-Term Stability of the Earth's Obliquity". Icarus. 50: 444–48. Bibcode:1982Icar...50..444W. doi:10.1016/0019-1035(82)90134-8.
- ↑ Touma, J.; Wisdom, J. (1993). "The Chaotic Obliquity of Mars" (PDF). Science. 259 (5099): 1294–1297. Bibcode:1993Sci...259.1294T. doi:10.1126/science.259.5099.1294. PMID 17732249.
- ↑ Correia, Alexandre C.M; Laskar, Jacques (2009). "Mercury's capture into the 3/2 spin-orbit resonance including the effect of core-mantle friction". Icarus. 201 (1): 1. arXiv:0901.1843
 . Bibcode:2009Icar..201....1C. doi:10.1016/j.icarus.2008.12.034.
. Bibcode:2009Icar..201....1C. doi:10.1016/j.icarus.2008.12.034. - ↑ Planetary Fact Sheets, at http://nssdc.gsfc.nasa.gov
- ↑ Astronomical Almanac 2010, p. B52, C3, D2, E3, E55
- ↑ Heller, R. "Holt-Rossiter-McLaughlin Encyclopaedia". René Heller. Retrieved 24 February 2012.
- ↑ Heller, R.; Leconte, J.; Barnes, R. (2011). "Tidal obliquity evolution of potentially habitable planets". Astronomy and Astrophysics. 528: A27. arXiv:1101.2156
 . Bibcode:2011A&A...528A..27H. doi:10.1051/0004-6361/201015809.
. Bibcode:2011A&A...528A..27H. doi:10.1051/0004-6361/201015809. - ↑ Heller, R.; Leconte, J.; Barnes, R. (2011). "Habitability of Extrasolar Planets and Tidal Spin Evolution". Origins of Life and Evolution of Biospheres: 37. Bibcode:2011OLEB..tmp...37H. doi:10.1007/s11084-011-9252-3.
External links
- National Space Science Data Center
- Seidelmann, P. Kenneth; Archinal, Brent A.; A'Hearn, Michael F.; et al. (2007). "Report of the IAU/IAG Working Group on cartographic coordinates and rotational elements: 2006". Celestial Mechanics and Dynamical Astronomy. 98 (3): 155–180. Bibcode:2007CeMDA..98..155S. doi:10.1007/s10569-007-9072-y.
- Obliquity of the Ecliptic Calculator
