Symmetry protected topological order
Symmetry Protected Topological order (SPT order)[1] is a kind of order in zero-temperature quantum-mechanical states of matter that have a symmetry and a finite energy gap.
To derive the results in a most-invariant way, renormalization group methods are used (leading to equivalence classes corresponding to certain fixed points).[1] The SPT order has the following defining properties:
(a) distinct SPT states with a given symmetry cannot be smoothly deformed into each other without a phase transition, if the deformation preserves the symmetry.
(b) however, they all can be smoothly deformed into the same trivial product state without a phase transition, if the symmetry is broken during the deformation.
The above definition works for both bosonic systems and fermionic systems, which leads to the notions of bosonic SPT order and fermionic SPT order.
Using the notion of quantum entanglement, we can say that SPT states are short-range entangled states with a symmetry (by contrast: for long-range entanglement see topological order, which is not related to the famous EPR paradox). Since short-range entangled states have only trivial topological orders we may also refer the SPT order as Symmetry Protected "Trivial" order.
Characteristic properties of SPT order
- The boundary effective theory of a non-trivial SPT state always has pure gauge anomaly or mixed gauge-gravity anomaly for the symmetry group.[2] As a result, the boundary of a SPT state is either gapless or degenerate, regardless how we cut the sample to form the boundary. A gapped non-degenerate boundary is impossible for a non-trivial SPT state. If the boundary is a gapped degenerate state, the degeneracy may be caused by spontaneous symmetry breaking and/or (intrinsic) topological order.
- Monodromy defects in non-trivial 2+1D SPT states carry non-trival statistics[3] and fractional quantum numbers[4] of the symmetry group. Monodromy defects are created by twisting the boundary condition along a cut by a symmetry transformation. The ends of such cut are the monodromy defects. For example, 2+1D bosonic Zn SPT states are classified by a Zn integer m. One can show that n identical elementary monodromy defects in a Zn SPT state labeled by m will carry a total Zn quantum number 2m which is not a multiple of n.
- 2+1D bosonic U(1) SPT states have a Hall conductance that is quantized as an even integer.[5][6][7] 2+1D bosonic SO(3) SPT states have a quantized spin Hall conductance.[8]
Relation between SPT order and (intrinsic) topological order
SPT states are short-range entangled while topologically ordered states are long-range entangled. Both intrinsic topological order, and also SPT order, can sometimes have protected gapless boundary excitations. The difference is subtle: the gapless boundary excitations in intrinsic topological order can be robust against any local perturbations, while the gapless boundary excitations in SPT order are robust only against local perturbations that do not break the symmetry. So the gapless boundary excitations in intrinsic topological order are topologically protected, while the gapless boundary excitations in SPT order are symmetry protected.[9]
We also know that an intrinsic topological order has emergent fractional charge, emergent fractional statistics, and emergent gauge theory. In contrast, a SPT order has no emergent fractional charge/fractional statistics for finite-energy excitations, nor emergent gauge theory (due to its short-range entanglement). Note that the monodromy defects discussed above are not finite-energy excitations in the spectrum of the Hamiltonian, but defects created by modifying the Hamiltonian.
Examples of SPT order
The first example of SPT order is the Haldane phase of spin-1 chain.[10] It is a SPT phase protected by SO(3) spin rotation symmetry.[1] A more well known example of SPT order is the topological insulator of non-interacting fermions, a SPT phase protected by U(1) and time reversal symmetry.
On the other hand, fractional quantum Hall states are not SPT states. They are states with (intrinsic) topological order and long-range entanglements.
Group cohomology theory for SPT phases
Using the notion of quantum entanglement, one obtains the following general picture of gapped phases at zero temperature. All gapped zero-temperature phases can be divided into two classes: long-range entangled phases (ie phases with intrinsic topological order) and short-range entangled phases (ie phases with no intrinsic topological order). All short-range entangled phases can be further divided into three classes: symmetry-breaking phases, SPT phases, and their mix (symmetry breaking order and SPT order can appear together).
It is well known that symmetry-breaking orders are described by group theory. For bosonic SPT phases with pure gauge anomalous boundary, it was shown that they are classified by group cohomology theory:[11] those (d+1)D SPT states with symmetry G are labeled by the elements in group cohomology class
![H^{d+1} [G, U(1)]](../I/m/8c315f440667cc062ba5376180aed9b3.png) .
For other (d+1)D SPT states[12] [13] with mixed gauge-gravity anomalous boundary, they can be described by
.
For other (d+1)D SPT states[12] [13] with mixed gauge-gravity anomalous boundary, they can be described by ![\oplus_{k=1}^d H^k[G,iTO^{d+1-k}]](../I/m/61f86758ae69175439f21f4d7a75e4bf.png) ,[14] where
,[14] where 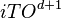 is the Abelian group formed by (d+1)D topologically ordered phases that have no non-trivial topological excitations (referred as iTO phases).
is the Abelian group formed by (d+1)D topologically ordered phases that have no non-trivial topological excitations (referred as iTO phases).
From the above results, many new quantum states of matter are predicted, including bosonic topological insulators (the SPT states protected U(1) and time-reversal symmetry) and bosonic topological superconductors (the SPT states protected by time-reversal symmetry), as well as many other new SPT states protected by other symmetries.
A list of bosonic SPT states from group cohomology ![H^{d+1} [G, U(1)]\oplus_{k=1}^d H^k[G,iTO^{d+1-k}]](../I/m/c66614d290ff8e42ee997f08e6a27b12.png) (
(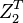 = time-reversal-symmetry group)
= time-reversal-symmetry group)
| symm. group | 1+1D | 2+1D | 3+1D | 4+1D | comment |
|---|---|---|---|---|---|
 |  | 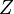 | 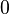 |  | iTO phases with no symmetry: 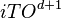 |
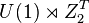 |  |  | 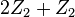 | 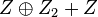 | bosonic topological insulator |
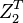 |  | 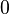 |  | 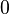 | bosonic topological superconductor |
 | 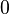 |  | 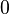 | 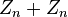 | |
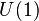 | 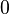 | 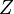 | 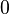 | 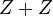 | 2+1D: quantum Hall effect |
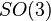 |  | 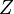 | 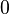 |  | 1+1D:Haldane phase; 2+1D: spin Hall effect |
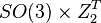 |  |  | 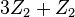 |  | |
 | 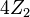 |  | 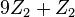 | 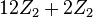 |
The phases before "+" come from ![H^{d+1} [G, U(1)]](../I/m/8c315f440667cc062ba5376180aed9b3.png) . The phases after "+" come from
. The phases after "+" come from ![\oplus_{k=1}^d H^k[G,iTO^{d+1-k}]](../I/m/61f86758ae69175439f21f4d7a75e4bf.png) .
Just like group theory can give us 230 crystal structures in 3+1D, group cohomology theory can give us various SPT phases in any dimensions with any on-site symmetry groups.
.
Just like group theory can give us 230 crystal structures in 3+1D, group cohomology theory can give us various SPT phases in any dimensions with any on-site symmetry groups.
On the other hand, the fermionic SPT orders are described by group super-cohomology theory.[15] So the group (super-)cohomology theory allows us to construct many SPT orders even for interacting systems, which include interacting topological insulator/superconductor.
A complete classification of 1D gapped quantum phases (with interactions)
Using the notions of quantum entanglement and SPT order, one can obtain a complete classification of all 1D gapped quantum phases.
First, it is shown that there is no (intrinsic) topological order in 1D (ie all 1D gapped states are short-range entangled).[16] Thus, if the Hamiltonians have no symmetry, all their 1D gapped quantum states belong to one phase—the phase of trivial product states. On the other hand, if the Hamiltonians do have a symmetry, their 1D gapped quantum states are either symmetry-breaking phases, SPT phases, and their mix.
Such an understanding allows one to classify all 1D gapped quantum phases:[11][17] All 1D gapped phases are classified by
the following three mathematical objects: ![(G_H, G_\Psi, H^{2} [G_\Psi , U(1)])](../I/m/055a50c3f6edfc48d71648578e36a0ea.png) , where
, where 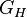 is the symmetry group of the Hamiltonian,
is the symmetry group of the Hamiltonian, 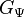 the symmetry group of the ground states, and
the symmetry group of the ground states, and ![H^{2} [G_\Psi, U(1)]](../I/m/a88cb5f3683d5179e92ab822a3310f94.png) the second group cohomology class of
the second group cohomology class of 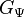 . (Note that
. (Note that ![H^{2} [G, U(1)]](../I/m/c101f541dcc2e35cbd16a5df2b01ae1b.png) classifies the projective representations of
classifies the projective representations of 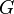 .) If there is no symmetry breaking (ie
.) If there is no symmetry breaking (ie  ), the 1D gapped phases are classified by the projective representations of symmetry group
), the 1D gapped phases are classified by the projective representations of symmetry group 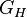 .
.
See also
References
- 1 2 3 Zheng-Cheng Gu, Xiao-Gang Wen, Tensor-Entanglement-Filtering Renormalization Approach and Symmetry Protected Topological Order , Phys. Rev. B80, 155131 (2009); Frank Pollmann, Erez Berg, Ari M. Turner, Masaki Oshikawa, Symmetry protection of topological order in one-dimensional quantum spin systems , Phys. Rev. B85, 075125 (2012).
- ↑ Xiao-Gang Wen, Classifying gauge anomalies through SPT orders and classifying gravitational anomalies through topological orders Phys. Rev. D 88, 045013 (2013); arXiv:1303.1803.
- ↑ Michael Levin, Zheng-Cheng Gu, Braiding statistics approach to symmetry-protected topological phases, Phys. Rev. B 86, 115109 (2012), arXiv:1202.3120.
- ↑ Xiao-Gang Wen, Topological invariants of symmetry-protected and symmetry-enriched topological phases of interacting bosons or fermions, arXiv:1301.7675.
- ↑ Yuan-Ming Lu, Ashvin Vishwanath, Theory and classification of interacting 'integer' topological phases in two dimensions: A Chern-Simons approach, Phys. Rev. B 86, 125119 (2012), arXiv:1205.3156.
- ↑ Peng Ye and Xiao-Gang Wen, "Projective construction of two-dimensional symmetry-protected topological phases with U(1), SO(3), or SU(2) symmetries", Phys. Rev. B 87, 195128 (2013). arXiv:1212.2121.
- ↑ Zheng-Xin Liu, Jia-Wei Mei, Peng Ye, and Xiao-Gang Wen, "U(1)×U(1) symmetry protected topological order in Gutzwiller wave functions", Phys. Rev. B 90, 235146 (2014), arXiv:1408.1676.
- ↑ Zheng-Xin Liu, Xiao-Gang Wen, Symmetry protected Spin Quantum Hall phases in 2-Dimensions, Phys. Rev. Lett. 110, 067205 (2013), arXiv:1205.7024.
- ↑ One should also note the semantical subtleness of the name SPT: "symmetry protected" does not mean that the stability of the state is conserved "because of the symmetry", but it is just meant that the symmetry is kept by the interactions corresponding to the process.
- ↑ F. D. M. Haldane, Phys. Rev. Lett. 50, 1153 (1983), Phys. Lett. 3,464 (1983); I. Affleck and F. D. M. Haldane, Pyhs. Rev. B 36, 5291 (1987); I. Affleck, J. Phys.: Condens. Matter. 1, 3047 (1989).
- 1 2 Xie Chen, Zheng-Xin Liu, Xiao-Gang Wen, 2D symmetry protected topological orders and their protected gapless edge excitations Phys. Rev. B 84, 235141 (2011); Xie Chen, Zheng-Cheng Gu, Zheng-Xin Liu, Xiao-Gang Wen, Symmetry protected topological orders and the group cohomology of their symmetry group
- ↑ Ashvin Vishwanath, T. Senthil; Physics of three dimensional bosonic topological insulators: Surface Deconfined Criticality and Quantized Magnetoelectric Effect Phys. Rev. X 3, 011016 (2013); arXiv:1209.3058.
- ↑ Peng Ye and Zheng-Cheng Gu, "Vortex-line condensation in three dimensions: A physical mechanism of bosonic topological insulators" Phys. Rev. X (2015); arXiv:1410.2594.
- ↑ Xiao-Gang Wen, Construction of bosonic symmetry-protected-trivial states and their topological terms via G×SO(∞) non-linear σ-models http://arxiv.org/abs/1410.8477
- ↑ Zheng-Cheng Gu, Xiao-Gang Wen, Symmetry-protected topological orders for interacting fermions -- fermionic topological non-linear sigma-models and a group super-cohomology theory
- ↑ F. Verstraete, J. I. Cirac, J. I. Latorre, E. Rico, and M. M. Wolf, Phys. Rev. Lett. 94, 140601 (2005).
- ↑ Xie Chen, Zheng-Cheng Gu, Xiao-Gang Wen, Classification of Gapped Symmetric Phases in 1D Spin Systems, Phys. Rev. B 83, 035107 (2011); Ari M. Turner, Frank Pollmann, Erez Berg, Topological Phases of One-Dimensional Fermions: An Entanglement Point of View, Phys. Rev. B.83.075102 (2011); Lukasz Fidkowski, Alexei Kitaev, Topological phases of fermions in one dimension, Phys. Rev. B.83.075103 (2011); N. Schuch, D. Perez-Garcia, and I. Cirac, Phys. Rev. B 84, 165139, (2011), arXiv:1010.3732.