Subsumption lattice
A subsumption lattice is a mathematical structure used in theoretical background of automated theorem proving and other symbolic computation applications.
Definition
A term t1 is said to subsume a term t2 if a substitution σ exists such that σ applied to t1 yields t2. In this case, t1 is also called more general than t2, and t2 is called more specific than t1, or an instance of t1.
The set of all (first-order) terms over a given signature can be made a lattice over the partial ordering relation "... is more specific than ..." as follows:
- consider two terms equal if they differ only in their variable naming,[1]
- add an artificial minimal element Ω (the overspecified term), which is considered to be more specific than any other term.
This lattice is called the subsumption lattice. Two terms are said to be unifiable if their meet differs from Ω.
Properties
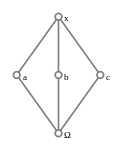
The join and the meet operation in this lattice are called anti-unification and unification, respectively. A variable x and the artificial element Ω are the top and the bottom element of the lattice, respectively. Each ground term, i.e.each term without variables, is an atom of the lattice. The lattice has infinite descending chains, e.g. x, g(x), g(g(x)), g(g(g(x))), ..., but no infinite ascending ones.
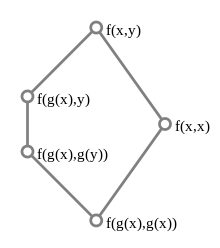
If f and g is a binary and unary function symbol, respectively, and x and y denote variables, then the terms f(x,y), f(g(x),y), f(g(x),g(y)), f(x,x), and f(g(x),g(x)) form the minimal non-modular lattice N5 (see pic.1); its appearance prevents the subsumption lattice from being modular and hence also from being distributive.
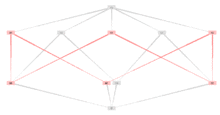
The set of terms unifiable with a given term need not be closed w.r.t. meet; pic.2 shows a counter-example.
Denoting by Gnd(t) the set of all ground instances of a term t, the following properties hold:[2]
- t equals the join of all members of Gnd(t), modulo renaming,
- t1 is an instance of t2 if and only if Gnd(t1) is a subset of Gnd(t2),
- terms with the same set of ground instances are equal modulo renaming,
- if t is the meet of t1 and t2, then Gnd(t) is the intersection of Gnd(t1) and Gnd(t2),
- if t is the join of t1 and t2, then Gnd(t) contains the union of Gnd(t1) and Gnd(t2).
Sublattice of linear terms
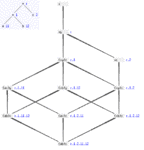 Pic.5: Distributive sublattice of linear terms |
 Pic.4: M3 built from linear terms |
 Pic.3: N5 built from linear terms |
The set of linear terms, that is of terms without multiple occurrences of a variable, is a sublattice of the subsumption lattice. This lattice, too, contains N5 and the minimal non-distributive lattice M3 as sublattices (see pic.3 and 4) and is hence not modular, let alone distributive.
The meet operation yields always the same result in the lattice of all terms and of linear terms. The join operation in all terms lattice yields always an instance of the join in the linear terms lattice; for example, the (ground) terms f(a,a) and f(b,b) have the join f(x,x) and f(x,y) in all terms lattice and in the linear terms lattice, respectively.
Join and meet of two proper[3] linear terms, i.e. their anti-unification and unification, corresponds to intersection and union of their path sets, respectively. Therefore, every sublattice of the lattice of linear terms that doesn't contain Ω is isomorphic to a set lattice, and hence distributive (see pic.5).
Origin
Apparently, the subsumption lattice has first been investigated by Gordon D. Plotkin in 1970.[4]
References
- ↑ formally: factorize the set of all terms by the equivalence relation "... is a renaming of ..."; for example, the term f(x,y) is a renaming of f(y,x), but not of f(x,x)
- ↑ Reynolds, John C. (1970). Meltzer, B.; Michie, D., eds. "Transformational Systems and the Algebraic Structure of Atomic Formulas" (PDF). Machine Intelligence. Edinburgh University Press. 5: 135–151.
- ↑ i.e. different from Ω
- ↑ Plotkin, Gordon D. (Jun 1970). Lattice Theoretic Properties of Subsumption. Edinburgh: Univ., Dept. of Machine Intell. and Perception.