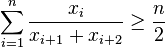Shapiro inequality

In mathematics, the Shapiro inequality is an inequality proposed by H. Shapiro in 1954.

Statement of the inequality

Suppose n is a natural number and 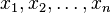$x_1, x_2, \dots, x_n$ are positive numbers and:

n is even and less than or equal to 12, or
n is odd and less than or equal to 23.

Then the Shapiro inequality states that

\sum_{i=1}^{n} \frac{x_i}{x_{i+1}+x_{i+2}} \geq \frac{n}{2}

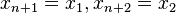where $x_{n+1}=x_1, x_{n+2}=x_2$ .

For greater values of n the inequality does not hold and the strict lower bound is 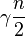$\gamma \frac{n}{2}$ with $\gamma \approx 0.9891\dots$ .

The initial proofs of the inequality in the pivotal cases n = 12 (Godunova and Levin, 1976) and n = 23 (Troesch, 1989) rely on numerical computations. In 2002, P.J. Bushell and J.B. McLeod published an analytical proof for n = 12.

The value of γ was determined in 1971 by Vladimir Drinfeld, who won a Fields Medal in 1990. Specifically, Drinfeld showed that the strict lower bound γ is given by 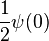$\frac{1}{2} \psi(0)$ , where ψ is the function convex hull of f(x) = e^−x and 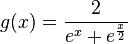$g(x) = \frac{2}{e^x+e^{\frac{x}{2}}}$ . (That is, the region above the graph of ψ is the convex hull of the union of the regions above the graphs of f and g.)

Interior local mimima of the left-hand side are always ≥ n/2 (Nowosad, 1968).

Counter-examples for higher n

The first counter-example was found by Lighthill in 1956, for n = 20:

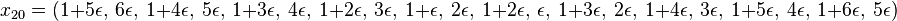x_{20} = (1+5\epsilon,\ 6\epsilon,\ 1+4\epsilon,\ 5\epsilon,\ 1+3\epsilon,\ 4\epsilon,\ 1+2\epsilon,\ 3\epsilon,\ 1+\epsilon,\ 2\epsilon,\ 1+2\epsilon,\ \epsilon,\ 1+3\epsilon,\ 2\epsilon,\ 1+4\epsilon,\ 3\epsilon,\ 1+5\epsilon,\ 4\epsilon,\ 1+6\epsilon,\ 5\epsilon)

where

\epsilon

is close to 0.

Then the left-hand side is equal to $10 - \epsilon^2 + O(\epsilon^3)$ , thus lower than 10 when $\epsilon$ is small enough.

The following counter-example for n = 14 is by Troesch (1985):

x_{14}

= (0, 42, 2, 42, 4, 41, 5, 39, 4, 38, 2, 38, 0, 40) (Troesch, 1985)

References

Fink, A.M. (1998). "Shapiro's inequality". In Gradimir V. Milovanović, G. V. Recent progress in inequalities. Dedicated to Prof. Dragoslav S. Mitrinović. Mathematics and its Applications (Dordrecht) 430. Dordrecht: Kluwer Academic Publishers. pp. 241–248. ISBN 0-7923-4845-1. Zbl 0895.26001.
Bushell, P.J.; McLeod, J.B. (2002). "Shapiro's cyclic inequality for even n" (PDF). J. Inequal. Appl. 7 (3): 331–348. ISSN 1029-242X. Zbl 1018.26010. They give an analytic proof of the formula for even n ≤ 12, from which the result for all n ≤ 12 follows. They state n = 23 as an open problem.

External links

Usenet discussion in 1999 (Dave Rusin's notes)
PlanetMath

This article is issued from Wikipedia - version of the 3/1/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.