S-wave
| Part of a series on |
| Earthquakes |
|---|
| Types |
|
|
| Causes |
| Characteristics |
|
|
| Measurement |
| Prediction |
|
|
| Other topics |
|
Earth Sciences Portal Category • Related topics |
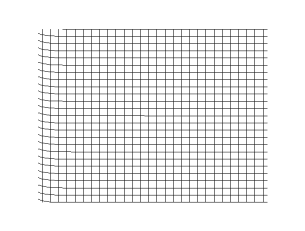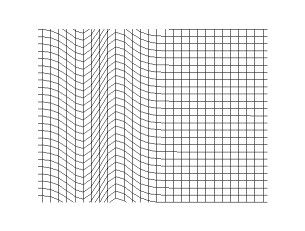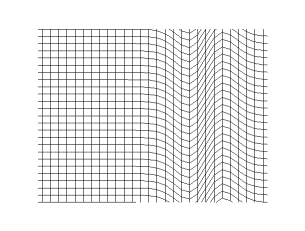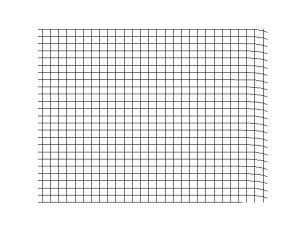
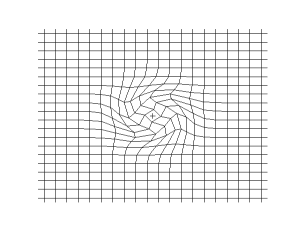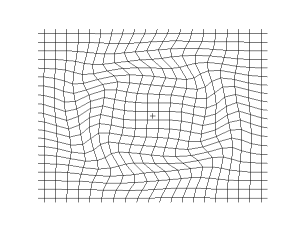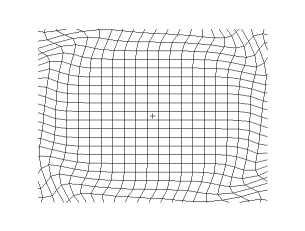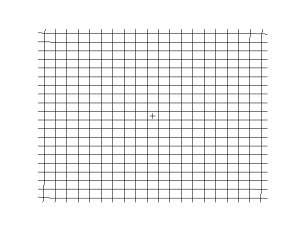
In seismology, S-waves, secondary waves, or shear waves (sometimes called an elastic S-wave) are a type of elastic wave, and are one of the two main types of elastic body waves, so named because they move through the body of an object, unlike surface waves.
The S-wave moves as a shear or transverse wave, so motion is perpendicular to the direction of wave propagation. The wave moves through elastic media, and the main restoring force comes from shear effects. These waves do not diverge, and they obey the continuity equation for incompressible media:
Its name, S for secondary, comes from the fact that it is the second direct arrival on an earthquake seismogram, after the compressional primary wave, or P-wave, because S-waves travel slower in rock. Unlike the P-wave, the S-wave cannot travel through the molten outer core of the Earth, and this causes a shadow zone for S-waves opposite to where they originate. They can still appear in the solid inner core: when a P-wave strikes the boundary of molten and solid cores, S-waves will then propagate in the solid medium. And when the S-waves hit the boundary again they will in turn create P-waves. This property allows seismologists to determine the nature of the inner core.[1]
As transverse waves, S-waves exhibit properties, such as polarization and birefringence, much like other transverse waves. S-waves polarized in the horizontal plane are classified as SH-waves. If polarized in the vertical plane, they are classified as SV-waves. When an S- or P-wave strikes an interface at an angle other than 90 degrees, a phenomenon known as mode conversion occurs. As described above, if the interface is between a solid and liquid, S becomes P or vice versa. However, even if the interface is between two solid media, mode conversion results. If a P-wave strikes an interface, four propagation modes may result: reflected and transmitted P and reflected and transmitted SV. Similarly, if an SV-wave strikes an interface, the same four modes occur in different proportions. The exact amplitudes of all these waves are described by the Zoeppritz equations, which in turn are solutions to the wave equation.
Theory
The prediction of S-waves came out of theory in the 1800s. Starting with the stress-strain relationship for an isotropic solid in Einstein notation:
where is the stress, and are the Lamé parameters (with as the shear modulus), is the Kronecker delta, and the strain tensor is defined
for strain displacement u. Plugging the latter into the former yields:
Newton's 2nd law in this situation gives the homogeneous equation of motion for seismic wave propagation:
where is the mass density. Plugging in the above stress tensor gives:
Applying vector identities and making certain approximations gives the seismic wave equation in homogeneous media:
where Newton's notation has been used for the time derivative. Taking the curl of this equation and applying vector identities eventually gives:
which is simply the wave equation applied to the curl of u with a velocity satisfying
This describes S-wave propagation. Taking the divergence of seismic wave equation in homogeneous media, instead of the curl, yields an equation describing P-wave propagation. The steady-state SH waves are defined by the Helmholtz equation
where k is the wave number.
See also
- Earthquake Early Warning (Japan)
- Lamb waves
- Longitudinal wave
- Love wave
- P-wave
- Rayleigh wave
- Seismic wave
- Shear wave splitting
- Surface wave
References
- ↑ University of Illinois at Chicago (17 July 1997). "Lecture 16 Seismographs and the earth's interior". Retrieved 8 June 2010.
- ↑ Sheikhhassani, Ramtin (2013). "Scattering of a plane harmonic SH wave by multiple layered inclusions". Wave Motion. 51 (3): 517–532. doi:10.1016/j.wavemoti.2013.12.002.
Further reading
- Shearer, Peter (1999). Introduction to Seismology (1st ed.). Cambridge University Press. ISBN 0-521-66023-8.
- Aki, Keiiti; Richards, Paul G. (2002). Quantitative Seismology (2nd ed.). University Science Books. ISBN 0-935702-96-2.
- Fowler, C. M. R. (1990). The solid earth. Cambridge, UK: Cambridge University Press. ISBN 0-521-38590-3.
