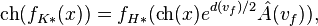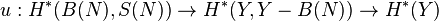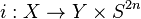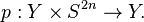Riemann–Roch theorem for smooth manifolds

In mathematics, a Riemann–Roch theorem for smooth manifolds is a version of results such as the Hirzebruch–Riemann–Roch theorem or Grothendieck–Riemann–Roch theorem (GRR) without a hypothesis making the smooth manifolds involved carry a complex structure. Results of this kind were obtained by Michael Atiyah and Friedrich Hirzebruch in 1959, reducing the requirements to something like a spin structure.

Formulation

Let X and Y be oriented smooth closed manifolds, and f: X → Y a continuous map. Let vf=f*(TY) − TX in the K-group K(X). If dim(X) ≡ dim(Y) mod 2, then

\mathrm{ch}(f_{K*}(x)) = f_{H*}(\mathrm{ch}(x) e^{d(v_f)/2}\hat{A}(v_f)),

where ch is the Chern character, d(vf) an element of the integral cohomology group H2(Y, Z) satisfying d(vf) ≡ f* w2(TY)-w2(TX) mod 2, fK* the Gysin homomorphism for K-theory, and fH* the Gysin homomorphism for cohomology .[1] This theorem was first proven by Atiyah and Hirzebruch.[2]

The theorem is proven by considering several special cases.[3] If Y is the Thom space of a vector bundle V over X, then the Gysin maps are just the Thom isomorphism. Then, using the splitting principle, it suffices to check the theorem via explicit computation for line bundles.

If f: X → Y is an embedding, then the Thom space of the normal bundle of X in Y can be viewed as a tubular neighborhood of X in Y, and excision gives a map

u:H^*(B(N), S(N)) \to H^*(Y, Y-B(N)) \to H^*(Y)

and

v:K(B(N), S(N)) \to K(Y, Y-B(N)) \to K(Y).

The Gysin map for K-theory/cohomology is defined to be the composition of the Thom isomorphism with these maps. Since the theorem holds for the map from X to the Thom space of N, and since the Chern character commutes with u and v, the theorem is also true for embeddings. f: X → Y.

Finally, we can factor a general map f: X → Y into an embedding

i: X \to Y \times S^{2n}

and the projection

p: Y \times S^{2n} \to Y.

The theorem is true for the embedding. The Gysin map for the projection is the Bott-periodicity isomorphism, which commutes with the Chern character, so the theorem holds in this general case also.

Corollaries

Atiyah and Hirzebruch then specialised and refined in the case X = a point, where the condition becomes the existence of a spin structure on Y. Corollaries are on Pontryagin classes and the J-homomorphism.

Notes

  1. ↑ M. Karoubi, K-theory, an introduction, Springer-Verlag, Berlin (1978)
  2. ↑ M. Atiyah and F. Hirzebruch, Riemann–Roch theorems for differentiable manifolds (Bull. Amer. Math. Soc. 65 (1959) 276–281)
  3. ↑ M. Karoubi, K-theory, an introduction, Springer-Verlag, Berlin (1978)
This article is issued from Wikipedia - version of the 3/22/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.