Representative elementary volume
In the theory of composite materials, the representative elementary volume (REV) (also called the representative volume element (RVE) or the unit cell) is the smallest volume over which a measurement can be made that will yield a value representative of the whole.[1] In the case of periodic materials, one simply chooses a periodic unit cell (which, however, may be non-unique), but in random media, the situation is much more complicated. For volumes smaller than the RVE, a representative property cannot be defined and the continuum description of the material involves Statistical Volume Element (SVE) and random fields. The property of interest can include mechanical properties such as elastic moduli, hydrogeological properties, electromagnetic properties, thermal properties, and other averaged quantities that are used to describe physical systems.
Definition

Rodney Hill defined the RVE as a sample of a heterogeneous material that:[3]
- "is entirely typical of the whole mixture on average”, and
- "contains a sufficient number of inclusions for the apparent properties to be independent of the surface values of traction and displacement, so long as these values are macroscopically uniform.”
In essence, statement (1) is about the material’s statistics (i.e. spatially homogeneous and ergodic), while statement (2) is a pronouncement on the independence of effective constitutive response with respect to the applied boundary conditions.
Both of these are issues of mesoscale (L) of the domain of random microstructure over which smoothing (or homogenization) is being done relative to the microscale (d).[4][5] As L/d goes to infinity, the RVE is obtained, while any finite mesoscale involves statistical scatter and, therefore, describes an SVE. With these considerations one obtains bounds on effective (macroscopic) response of elastic (non)linear and inelastic random microstructures.[6] In general, the stronger the mismatch in material properties, or the stronger the departure from elastic behavior, the larger is the RVE. The finite-size scaling of elastic material properties from SVE to RVE can be grasped in compact forms with the help of scaling functions universally based on stretched exponentials.[7] Considering that the SVE may be placed anywhere in the material domain, one arrives at a technique for characterization of continuum random fields.[8]
Another definition of the RVE was proposed by Drugan and Willis:
- "It is the smallest material volume element of the composite for which the usual spatially constant (overall modulus) macroscopic constitutive representation is a sufficiently accurate model to represent mean constitutive response." [9][10][11]
The choice of RVE can be quite a complicated process. The existence of a RVE assumes that it is possible to replace a heterogeneous material with an equivalent homogeneous material. This assumption implies that the volume should be large enough to represent the microstructure without introducing non-existing macroscopic properties (such as anisotropy in a macroscopically isotropic material). On the other hand, the sample should be small enough to be analyzed analytically or numerically.
Examples
RVEs for mechanical properties


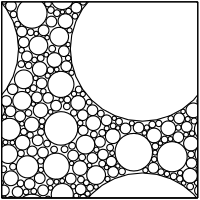
In continuum mechanics generally for a heterogeneous material, RVE can be considered as a volume V that represents a composite statistically, i.e., volume that effectively includes a sampling of all microstructural heterogeneities (grains, inclusions, voids, fibers, etc.) that occur in the composite. It must however remain small enough to be considered as a volume element of continuum mechanics. Several types of boundary conditions can be prescribed on V to impose a given mean strain or mean stress to the material element.[14]
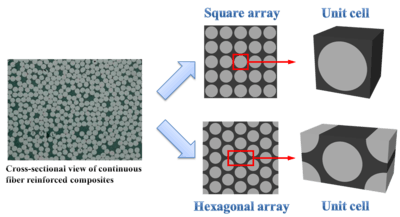
Analytical or numerical micromechanical analysis of fiber reinforced composites involves the study of a representative volume element (RVE). Although fibers are distributed randomly in real composites, many micromechanical models assume periodic arrangement of fibers from which RVE can be isolated in a straightforward manner. The RVE has the same elastic constants and fiber volume fraction as the composite.[15] In general RVE can be considered same as a differential element with a large number of crystals.
RVEs for porous media
In order to establish a given porous medium's properties, we are going to have to measure samples of the porous medium. If the sample is too small, the readings tend to oscillate. As we increase the sample size, the oscillations begin to dampen out. Eventually the sample size will become large enough that we begin to get consistent readings. This sample size is referred to as the representative elementary volume. If we continue to increase our sample size, measurement will remain stable until the sample size gets large enough that we begin to include other hydrostratigraphic layers. This is referred to as the maximum elementary volume (MEV).
Groundwater flow equation has to be defined in an REV.
RVEs for electromagnetic media


While RVEs for electromagnetic media can have the same form as those for elastic or porous media, the fact that mechanical strength and stability are not concerns allow for a wide range of RVEs. In the adjacent figure, the RVE consists of a split-ring resonator and its surrounding backing material.
Alternatives for RVE
There does not exist one RVE size and depending on the studied mechanical properties, the RVE size can vary significantly. The concept of statistical volume element (SVE) and uncorrelated volume element (UVE) have been introduced as alternatives for RVE.
Statistical Volume Element (SVE)
Statistical volume element (SVE), which is also referred to as stochastic volume element in finite element analysis, takes into account the variability in the microstructure. Unlike RVE in which average value is assumed for all realizations, SVE can have a different value from one realization to another. SVE models have been developed to study polycrystalline microstructures. Grain features, including orientation, misorientation, grain size, grain shape, grain aspect ratio are considered in SVE model. SVE model was applied in the material characterization and damage prediction in microscale. Compared with RVE, SVE can provide a comprehensive representation of the microstructure of materials.[16][17]
Uncorrelated Volume Element (UVE)
Uncorrelated volume element (UVE) is an extension of SVE which also considers the co-variance of adjacent microstructure to present an accurate length scale for stochastic modelling.[18]
References
- ↑ Hill (1963)
- ↑ Banerjee (2005)
- ↑ Hill (1963)
- ↑ Huet (1990)
- ↑ Sab (1992)
- ↑ Ostoja-Starzewski (2008)
- ↑ Ranganathan and Ostoja-Starzewski (2008)
- ↑ Sena, Ostoja-Starzewski and Costa (2013)
- ↑ Drugan and Willis (1996).
- ↑ Kanit et al. (2003)
- ↑ Lydzba and Rozanski (2014)
- ↑ Banerjee (2003)
- ↑ Banerjee (2005)
- ↑ Kanit et al (2003).
- ↑ Sun and Vaidya (1996).
- ↑ Zhang, Jinjun (2013). "Crack initiation and fatigue life prediction on aluminum lug joints using statistical volume element–based multiscale modeling". Journal of Intelligent Material Systems and Structures. 24 (17): 2097–2109.
- ↑ Zhang, Jinjun (2014). "Physics‐based multiscale damage criterion for fatigue crack prediction in aluminium alloy". Fatigue & Fracture of Engineering Materials & Structures. 37 (2): 119–131.
- ↑ Sanei and Fertig (2015)
Bibliography
- Hill, R. (1963), "Elastic properties of reinforced solids: some theoretical principles." (PDF), Journal of the Mechanics and Physics of Solids, 11 (5): 357–372, doi:10.1016/0022-5096(63)90036-x
- Huet, C. (1990), "Application of variational concepts to size effects in elastic heterogeneous bodies", Journal of the Mechanics and Physics of Solids, 38: 813–841, doi:10.1016/0022-5096(90)90041-2
- Sab, K. (1992), "On the homogenization and the simulation of random materials", European Journal of Mechanics, A/Solids, 11,c: 585–607
- Ostoja-Starzewski, M. (2008). Microstructural Randomness and Scaling in Mechanics of Materials. Chapman & Hall/CRC Press.
- Ranganathan, S. J.; Ostoja-Starzewski, M. (2008), "Scaling function, anisotropy and the size of RVE in elastic random polycrystals" (PDF), Journal of the Mechanics and Physics of Solids, 56: 2773–2791, doi:10.1016/j.jmps.2008.05.001
- Sena, M. P.; Ostoja-Starzewski, M.; Ostoja-Starzewski, M. (2013), "Stiffness tensor random fields through upscaling of planar random materials" (PDF), Probabilistic Eng. Mech., 34: 131–156, doi:10.1016/j.probengmech.2013.08.008
- Drugan, W. J.; Willis, J. R. (1996), "A micromechanics-based nonlocal constitutive equation and estimates of representative volume element size for elastic composites", Journal of the Mechanics and Physics of Solids, 44 (4): 497–524, doi:10.1016/0022-5096(96)00007-5
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. (2003), "Determination of the size of the representative volume element for random composites: statistical and numerical approach", International Journal of Solids and Structures, 40: 3647–3679., doi:10.1016/s0020-7683(03)00143-4
- Sun, C. T.; Vaidya, R. S. (1996), "Prediction of composite properties from a representative volume element", Composites Science and Technology, 56: 171–179., doi:10.1016/0266-3538(95)00141-7
- Banerjee, Biswajit; Cady, Carl M.; Adams., Daniel O. (2003), "Micromechanics simulations of glass–estane mock polymer bonded explosives.", Modelling and Simulation in Materials Science and Engineering, 11 (4): 457–475, doi:10.1088/0965-0393/11/4/304
- Banerjee, Biswajit (2005), Effective elastic moduli of polymer bonded explosives from finite element simulations (PDF), arXiv:cond-mat/0510367
 .
. - Lydzba, D.; Rozanski, A. (2014), "Microstructure Measures and the Minimum Size of a Representative Volume Element: 2D Numerical Study", Acta Geophysica, 62 (5): 1060–1086, doi:10.2478/s11600-014-0226-5
- Sanei, S.; Fertig, R. (2015), "Uncorrelated volume element for stochastic modeling of microstructures based on local fiber volume fraction variation", Composites Science and Technology, 117: 191–198, doi:10.1016/j.compscitech.2015.06.010