Plethystic substitution

Plethystic substitution is a shorthand notation for a common kind of substitution in the algebra of symmetric functions and that of symmetric polynomials. It is essentially basic substitution of variables, but allows for a change in the number of variables used.

Definition

The formal definition of plethystic substitution relies on the fact that the ring of symmetric functions 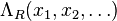$\Lambda_R(x_1,x_2,\ldots)$ is generated as an R-algebra by the power sum symmetric functions

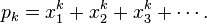
$p_k=x_1^k+x_2^k+x_3^k+\cdots.$

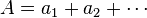For any symmetric function $f$ and any formal sum of monomials $A=a_1+a_2+\cdots$ , the plethystic substitution f[A] is the formal series obtained by making the substitutions

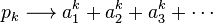
$p_k \longrightarrow a_1^k+a_2^k+a_3^k+\cdots$

in the decomposition of $f$ as a polynomial in the p_k's.

Examples

If 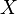$X$ denotes the formal sum $X=x_1+x_2+\cdots$ , then $f[X]=f(x_1,x_2,\ldots)$ .

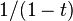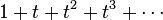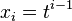One can write $1/(1-t)$ to denote the formal sum $1+t+t^2+t^3+\cdots$ , and so the plethystic substitution $f[1/(1-t)]$ is simply the result of setting $x_i=t^{i-1}$ for each i. That is,

$f\left[\frac{1}{1-t}\right]=f(1,t,t^2,t^3,\ldots)$ .

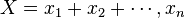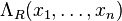Plethystic substitution can also be used to change the number of variables: if $X=x_1+x_2+\cdots,x_n$ , then $f[X]=f(x_1,\ldots,x_n)$ is the corresponding symmetric function in the ring $\Lambda_R(x_1,\ldots,x_n)$ of symmetric functions in n variables.

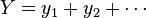Several other common substitutions are listed below. In all of the following examples, $X=x_1+x_2+\cdots$ and $Y=y_1+y_2+\cdots$ are formal sums.

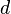If $f$ is a homogeneous symmetric function of degree $d$ , then

$f[tX]=t^d f(x_1,x_2,\ldots)$

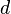If $f$ is a homogeneous symmetric function of degree $d$ , then

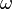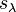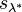$f[-X]=(-1)^d \omega f(x_1,x_2,\ldots)$ , where $\omega$ is the well-known involution on symmetric functions that sends a Schur function $s_{\lambda}$ to the conjugate Schur function $s_{\lambda^\ast}$ .

The substitution $S:f\mapsto f[-X]$ is the antipode for the Hopf algebra structure on the Ring of symmetric functions.
$p_n[X+Y]=p_n[X]+p_n[Y]$
The map $\Delta: f\mapsto f[X+Y]$ is the coproduct for the Hopf algebra structure on the ring of symmetric functions.
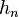$h_n\left[X(1-t)\right]$ is the alternating Frobenius series for the exterior algebra of the defining representation of the symmetric group, where $h_n$ denotes the complete homogeneous symmetric function of degree $n$ .
$h_n\left[X/(1-t)\right]$ is the Frobenius series for the symmetric algebra of the defining representation of the symmetric group.

External links

Combinatorics, Symmetric Functions, and Hilbert Schemes (Haiman, 2002)

References

M. Haiman, Combinatorics, Symmetric Functions, and Hilbert Schemes, Current Developments in Mathematics 2002, no. 1 (2002), pp. 39–111.

This article is issued from Wikipedia - version of the 4/6/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.