Pascal's law
| Continuum mechanics | ||||
|---|---|---|---|---|
 | ||||
|
Laws
|
||||
Pascal's law or the principle of transmission of fluid-pressure (also Pascal's Principle[1][2][3]) is a principle in fluid mechanics that states that a pressure change occurring anywhere in a confined incompressible fluid is transmitted throughout the fluid such that the same change occurs everywhere.[4] The law was established by French mathematician Blaise Pascal.[5]
Definition
.svg.png)
Pascal's principle is defined as
A change in pressure at any point in an enclosed fluid at rest is transmitted undiminished to all points in the fluid.
This principle is stated mathematically as:
- is the hydrostatic pressure (given in pascals in the SI system), or the difference in pressure at two points within a fluid column, due to the weight of the fluid;
- ρ is the fluid density (in kilograms per cubic meter in the SI system);
- g is acceleration due to gravity (normally using the sea level acceleration due to Earth's gravity, in SI in metres per second squared);
- is the height of fluid above the point of measurement, or the difference in elevation between the two points within the fluid column (in metres in SI).
The intuitive explanation of this formula is that the change in pressure between 2 elevations is due to the weight of the fluid between the elevations. A more correct interpretation, though, is that the pressure change is caused by the change of potential energy per unit volume of the liquid due to the existence of the gravitational field. Note that the variation with height does not depend on any additional pressures. Therefore, Pascal's law can be interpreted as saying that any change in pressure applied at any given point of the fluid is transmitted undiminished throughout the fluid.
Explanation
If a U-tube is filled with water and pistons are placed at each end, pressure exerted against the left piston will be transmitted throughout the liquid and against the bottom of the right piston. (The pistons are simply "plugs" that can slide freely but snugly inside the tube.) The pressure that the left piston exerts against the water will be exactly equal to the pressure the water exerts against the right piston. Suppose the tube on the right side is made wider and a piston of a larger area is used; for example, the piston on the right has 50 times the area of the piston on the left. If a 1 N load is placed on the left piston, an additional pressure due to the weight of the load is transmitted throughout the liquid and up against the larger piston. The difference between force and pressure is important: the additional pressure is exerted against the entire area of the larger piston. Since there is 50 times the area, 50 times as much force is exerted on the larger piston. Thus, the larger piston will support a 50 N load - fifty times the load on the smaller piston.
Forces can be multiplied using such a device. One newton input produces 50 newtons output. By further increasing the area of the larger piston (or reducing the area of the smaller piston), forces can be multiplied, in principle, by any amount. Pascal's principle underlies the operation of the hydraulic press. The hydraulic press does not violate energy conservation, because a decrease in distance moved compensates for the increase in force. When the small piston is moved downward 100 centimeters, the large piston will be raised only one-fiftieth of this, or 2 centimeters. The input force multiplied by the distance moved by the smaller piston is equal to the output force multiplied by the distance moved by the larger piston; this is one more example of a simple machine operating on the same principle as a mechanical lever.
Pascal's principle applies to all fluids, whether gases or liquids. A typical application of Pascal's principle for gases and liquids is the automobile lift seen in many service stations (the hydraulic jack). Increased air pressure produced by an air compressor is transmitted through the air to the surface of oil in an underground reservoir. The oil, in turn, transmits the pressure to a piston, which lifts the automobile. The relatively low pressure that exerts the lifting force against the piston is about the same as the air pressure in automobile tires. Hydraulics is employed by modern devices ranging from very small to enormous. For example, there are hydraulic pistons in almost all construction machines where heavy loads are involved.
Pascal's barrel
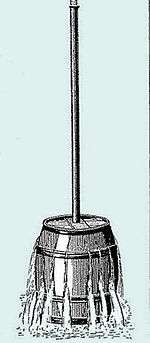
Pascal's barrel is the name of a hydrostatics experiment allegedly performed by Blaise Pascal in 1646.[6] In the experiment, Pascal inserted a 10-m long (32.8 ft) vertical tube into a barrel filled with water.[7] When water was poured into the vertical tube, Pascal found that the increase in hydrostatic pressure caused the barrel to burst.[6]
The experiment is mentioned nowhere in Pascal's preserved works and it may be apocryphal, attributed to him by 19th-century French authors, among whom the experiment is known as crève-tonneau (approx.: "barrel-buster");[8] nevertheless the experiment remains associated with Pascal in many elementary physics textbooks.[9]
Applications of Pascal's law
- The underlying principle of the hydraulic jack and hydraulic press.
- Force amplification in the braking system of most motor vehicles.
- Used in artesian wells, water towers, and dams.
- Scuba divers must understand this principle. At a depth of 10 meters under water, pressure is twice the atmospheric pressure at sea level, and increases by about 100 kPa for each increase of 10 m depth.[5]
- Usually Pascal's rule is applied to confined space (static flow), but due to the continuous flow process, Pascal's principle can be applied to the lift oil mechanism (which can be represented as a U tube with pistons on either end). However, the lift height will be in microns because energy will be drained and pressure will be diminished after each impact with the lifting material, but force exerted will be equal.
- Applied force in cylinder P1A1.
- The underlying principal of hot isostatic pressing
See also
References
- ↑ http://www.britannica.com/EBchecked/topic/445445/Pascals-principle
- ↑ https://www.grc.nasa.gov/www/k-12/WindTunnel/Activities/Pascals_principle.html
- ↑ http://hyperphysics.phy-astr.gsu.edu/hbase/pasc.html
- ↑ Bloomfield, Louis (2006). How Things Work: The Physics of Everyday Life (Third Edition). John Wiley & Sons. p. 153. ISBN 0-471-46886-X.
- 1 2 Acott, Chris (1999). "The diving "Law-ers": A brief resume of their lives.". South Pacific Underwater Medicine Society journal. 29 (1). ISSN 0813-1988. OCLC 16986801. Retrieved 2011-06-14..
- 1 2 Merriman, Mansfield (1903). Treatise on hydraulics (8 ed.). J. Wiley. p. 22.
- ↑ Wine East. 22-23. L & H Photo Journalism. 1994. p. 23.
- ↑ perhaps first in an educational context; the attribution is found under this name in A. Merlette, L'encyclopédie des écoles, journal de l'enseignement primaire et professionnel (1863) p. 284: l'expérience du crève-tonneau réalisée pour la première fois par le célèbre Biaise Pascal. Ernest Menu de Saint-Mesmin, Problèmes de mathématiques et de physique: donnés dans les Facultés des science et notamment à la Sorbonne, avec les solutions raisonnées, L. Hachette (1862), p. 380.
- ↑ see e.g. E. Canon-Tapia in: Thor Thordarson (ed.) Studies in Volcanology, 2009, ISBN 9781862392809, p. 273.