Novikov's compact leaf theorem

In mathematics, Novikov's compact leaf theorem, named after Sergei Novikov, states that

A codimension-one foliation of a compact 3-manifold whose universal covering space is not contractible must have a compact leaf.

Novikov's compact leaf theorem for S³

Theorem: A smooth codimension-one foliation of the 3-sphere S³ has a compact leaf. The leaf is a torus T² bounding a solid torus with the Reeb foliation.

The theorem was proved by Sergey Novikov in 1964. Earlier Charles Ehresmann had conjectured that every smooth codimension-one foliation on S³ had a compact leaf, which was true for all known examples; in particular, the Reeb foliation had a compact leaf that was T².

Novikov's compact leaf theorem for any M³

In 1965, Novikov proved the compact leaf theorem for any M³:

Theorem: Let M³ be a closed 3-manifold with a smooth codimension-one foliation F. Suppose any of the following conditions is satisfied:

1. the fundamental group is finite,
2. the second homotopy group ,
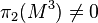3. there exists a leaf 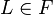such that the map induced by inclusion has a non-trivial kernel.

Then F has a compact leaf of genus g ≤ 1.

In terms of covering spaces:

A codimension-one foliation of a compact 3-manifold whose universal covering space is not contractible must have a compact leaf.

References

• S. Novikov. The topology of foliations//Trudy Moskov. Mat. Obshch, 1965, v. 14, p. 248–278.
• I. Tamura. Topology of foliations — AMS, v.97, 2006.
• D. Sullivan, Cycles for the dynamical study of foliated manifolds and complex manifolds, Invent. Math., 36 (1976), p. 225–255.