Mutual exclusion
In computer science, mutual exclusion is a property of concurrency control, which is instituted for the purpose of preventing race conditions; it is the requirement that one thread of execution never enter its critical section at the same time that another concurrent thread of execution enters its own critical section.[lower-alpha 1]
The requirement of mutual exclusion was first identified and solved by Edsger W. Dijkstra in his seminal 1965 paper titled Solution of a problem in concurrent programming control,[1][2] which is credited as the first topic in the study of concurrent algorithms.[3]
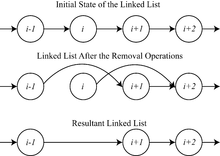
A simple example of why mutual exclusion is important in practice can be visualized using a singly linked list of four items, where the second and third are to be removed. The removal of a node that sits between 2 other nodes is performed by changing the next pointer of the previous node to point to the next node (in other words, if node i is being removed, then the next pointer of node i − 1 is changed to point to node i + 1, thereby removing from the linked list any reference to node i). When such a linked list is being shared between multiple threads of execution, two threads of execution may attempt to remove two different nodes simultaneously, one thread of execution changing the next pointer of node i − 1 to point to node i + 1, while another thread of execution changes the next pointer of node i to point to node i + 2. Although both removal operations complete successfully, the desired state of the linked list is not achieved: node i + 1 remains in the list, because the next pointer of node i − 1 points to node i + 1.
This problem (called a race condition) can be avoided by using the requirement of mutual exclusion to ensure that simultaneous updates to the same part of the list cannot occur.
Problem description
The problem of mutual exclusion involves resources allocation among n processes and makes sure those resources cannot be used simultaneously by more than a single process. To have the access to those resources, each process is required to execute the code segment called the critical section. The property required that at any time at most one processor is in the critical section is called mutual exclusion. And at any time, if at least one process is trying to enter the critical section, then at some later point, one of them can enter the critical section successfully as long as no processor stays in the critical section forever. Such property is called no deadlock. A stronger property provides the no deadlock guarantee on individual basis. This stronger property is called no lockout and it guarantees that if a process wish to enter the critical section, it will enter the critical section successfully at some later point as long as no processor stays in the critical section forever. Although the no lockout property ensures that every process which wishes to access the critical section will eventually succeed, a process can be overtaken an unbounded number of time before it finally enters the critical section. A k-bounded waiting property can provide a bounded waiting guarantee and it requires in every execution, a process can only enter the critical section at most k times while another process is waiting to enter the critical section.
The program of each process can be partitioned into four sections:[4]
- Non-Critical Section
- processes do not try to enter the critical section in this section.
- Trying
- processes attempt to enter the critical section in this section.
- Critical Section
- a process is allowed to access the shared resources in this section.
- Exit
- a process leaves the critical section and makes the critical section available to other processes.
Each process can cyclically enter the above sections in this order: Non-Critical Section, Trying, Critical Section, Exit. If a process wishes to enter the critical section, it need to execute the trying section and wait until it acquires the access to the critical section. After process enter the critical section and done with the shared resources, it need to execute the exit section and release the critical section. After that, the process return to the non-critical section.
Enforcing mutual exclusion
There are both software and hardware solutions for enforcing mutual exclusion. Some different solutions are discussed below.
Hardware solutions
On uniprocessor systems, the simplest solution to achieve mutual exclusion is to disable interrupts during a process's critical section. This will prevent any interrupt service routines from running (effectively preventing a process from being preempted). Although this solution is effective, it leads to many problems. If a critical section is long, then the system clock will drift every time a critical section is executed because the timer interrupt is no longer serviced, so tracking time is impossible during the critical section. Also, if a process halts during its critical section, control will never be returned to another process, effectively halting the entire system. A more elegant method for achieving mutual exclusion is the busy-wait.
Busy-waiting is effective for both uniprocessor and multiprocessor systems. The use of shared memory and an atomic test-and-set instruction provides the mutual exclusion. A process can test-and-set on a location in shared memory, and since the operation is atomic, only one process can set the flag at a time. Any process that is unsuccessful in setting the flag can either go on to do other tasks and try again later, release the processor to another process and try again later, or continue to loop while checking the flag until it is successful in acquiring it. Preemption is still possible, so this method allows the system to continue to function—even if a process halts while holding the lock.
Several other atomic operations can be used to provide mutual exclusion of data structures; most notable of these is compare-and-swap (CAS). CAS can be used to achieve wait-free mutual exclusion for any shared data structure by creating a linked list where each node represents the desired operation to be performed. CAS is then used to change the pointers in the linked list[5] during the insertion of a new node. Only one process can be successful in its CAS; all other processes attempting to add a node at the same time will have to try again. Each process can then keep a local copy of the data structure, and upon traversing the linked list, can perform each operation from the list on its local copy.
Software solutions
Beside hardware-supported solutions, some software solutions exist that use busy waiting to achieve mutual exclusion. Examples of these include the following:
- Dekker's algorithm;
- Peterson's algorithm;
- Lamport's bakery algorithm;[6]
- Szymanski's algorithm;
- Taubenfeld's black-white bakery algorithm.[2]
These algorithms do not work if out-of-order execution is used on the platform that executes them. Programmers have to specify strict ordering on the memory operations within a thread.[7]
It is often preferable to use synchronization facilities provided by an operating system's multithreading library, which will take advantage of hardware solutions if possible but will use software solutions if no hardware solutions exist. For example, when the operating system's lock library is used and a thread tries to acquire an already acquired lock, the operating system could suspend the thread using a context switch and swap it out with another thread that is ready to be run, or could put that processor into a low power state if there is no other thread that can be run. Therefore, most modern mutual exclusion methods attempt to reduce latency and busy-waits by using queuing and context switches. However, if the time that is spent suspending a thread and then restoring it can be proven to be always more than the time that must be waited for a thread to become ready to run after being blocked in a particular situation, then spinlocks are an acceptable solution (for that situation only).
Bound on the mutual exclusion problem
One binary test&set register is sufficient to provide the deadlock-free solution to the mutual exclusion problem. But the solution built by test&set register can possibly lead to the starvation of some processes in the trying section.[8] In fact, distinct memory states are required to avoid lockout. And to avoid the unbounded waiting, n distinct memory states are required.[9]:
Types of mutual exclusion devices
The solutions explained above can be used to build the synchronization primitives below:
Many forms of mutual exclusion have side-effects. For example, classic semaphores permit deadlocks, in which one process gets a semaphore, another process gets a second semaphore, and then both wait forever for the other semaphore to be released. Other common side-effects include starvation, in which a process never gets sufficient resources to run to completion; priority inversion, in which a higher priority thread waits for a lower-priority thread; and high latency, in which response to interrupts is not prompt.
Much research is aimed at eliminating the above effects, often with the goal of guaranteeing non-blocking progress. No perfect scheme is known. Blocking system calls used to sleep an entire process. Until such calls became threadsafe, there was no proper mechanism for sleeping a single thread within a process (see polling).
See also
- Atomicity (programming)
- Concurrency control
- Exclusive or
- Mutually exclusive events
- Semaphore
- Dining philosophers problem
- Reentrant mutex
- Spinlock
Notes
- ↑ Here, critical section refers to an interval of time during which a thread of execution accesses a shared resource, such as shared memory.
References
- ↑ Dijkstra, E. W. (1965). "Solution of a problem in concurrent programming control". Communications of the ACM. 8 (9): 569. doi:10.1145/365559.365617.
- 1 2 Taubenfeld, The Black-White Bakery Algorithm. In Proc. Distributed Computing, 18th international conference, DISC 2004. Vol 18, 56-70, 2004
- ↑ "PODC Influential Paper Award: 2002", ACM Symposium on Principles of Distributed Computing, retrieved 2009-08-24
- ↑ Lamport, Leslie (June 26, 2000), The Mutual Exclusion Problem Part II: Statement and Solutions (PDF)
- ↑ https://timharris.uk/papers/2001-disc.pdf
- ↑ Lamport, Leslie (August 1974). "A new solution of Dijkstra's concurrent programming problem". Communications of the ACM. 17 (8): 453–455. doi:10.1145/361082.361093.
- ↑ Holzmann, Gerard J.; Bosnacki, Dragan (1 October 2007). "The Design of a Multicore Extension of the SPIN Model Checker". IEEE Transactions on Software Engineering. 33 (10): 659–674. doi:10.1109/TSE.2007.70724.
- ↑ Attiya, Hagit; Welch, Jennifer (Mar 25, 2004). Distributed computing: fundamentals, simulations, and advanced topics. John Wiley & Sons, Inc. ISBN 978-0-471-45324-6.
- ↑ Burns, James E.; Paul Jackson, Nancy A. Lynch (January 1982), Data Requirements for Implementation of N-Process Mutual Exclusion Using a Single Shared Variable (PDF)
Further reading
- Michel Raynal: Algorithms for Mutual Exclusion, MIT Press, ISBN 0-262-18119-3
- Sunil R. Das, Pradip K. Srimani: Distributed Mutual Exclusion Algorithms, IEEE Computer Society, ISBN 0-8186-3380-8
- Thomas W. Christopher, George K. Thiruvathukal: High-Performance Java Platform Computing, Prentice Hall, ISBN 0-13-016164-0
- Gadi Taubenfeld, Synchronization Algorithms and Concurrent Programming, Pearson/Prentice Hall, ISBN 0-13-197259-6
External links
- Article A Simple Mutex Program
- Common threads: POSIX threads explained - The little things called mutexes" by Daniel Robbins
- Mutual Exclusion Petri Net
- Mutual Exclusion with Locks - an Introduction
- Mutual exclusion variants in OpenMP
- The Black-White Bakery Algorithm