Matsubara frequency
In thermal quantum field theory, the Matsubara frequency summation (named after Takeo Matsubara) is the summation over discrete imaginary frequencies. It takes the following form
- ,
where is the inverse temperature and the frequencies are usually taken from either of the following two sets (with ):
- bosonic frequencies: ,
- fermionic frequencies: .
The summation will converge if g(z=iω) tends to 0 in z→∞ limit in a manner faster than . The summation over bosonic frequencies is denoted as SB (with η=+1), while that over fermionic frequencies is denoted as SF (with η=-1). η is the statistical sign.
In addition to thermal quantum field theory, the Matsubara frequency summation method plays also an essential role in the diagrammatic approach to solid-state physics, namely, if one considers the diagrams at finite temperature.[1]
Generally speaking, if at T=0 K a certain Feynman diagram is represented by an integral , at finite temperature it is given by the sum .
Matsubara Frequency Summation
General Formalism
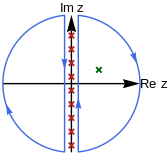

The trick to evaluate Matsubara frequency summation is to use a Matsubara weighting function hη(z) that has simple poles located exactly at . The weighting functions in the boson case η=+1 and fermion case η=-1 differ. The choice of weighting function will be discussed later. With the weighting function, the summation can be replaced by a contour integral in the complex plane.
- .
As in Fig. 1, the weighting function generates poles (red crosses) on the imaginary axis. The contour integral picks up the residue of these poles, which is equivalent to the summation.
By deformation of the contour lines to enclose the poles of g(z) (the green cross in Fig. 2), the summation can be formally accomplished by summing the residue of g(z)hη(z) over all poles of g(z),
- .
Note that a minus sign is produced, because the contour is deformed to enclose the poles in the clockwise direction, resulting in the negative residue.
Choice of Matsubara Weighting Function
To produce simple poles on boson frequencies , either of the following two types of Matsubara weighting functions can be chosen
- ,
- ,
depending on which half plane the convergence is to be controlled in. controls the convergence in the left half plane (Re z<0), while controls the convergence in the right half plane (Re z>0). Here is the Bose–Einstein distribution function.
The case is similar for fermion frequencies. There are also two types of Matsubara weighting functions that produce simple poles at
- ,
- .
controls the convergence in the left half plane (Re z<0), while controls the convergence in the right half plane (Re z>0). Here is the Fermi–Dirac distribution function.
In the application to Green's function calculation, g(z) always have the structure
- ,
which diverges in the left half plane given 0<τ<β. So as to control the convergence, the weighting function of the first type is always chosen . However there is no need to control the convergence if the Matsubara summation does not diverge, in that case, any choice of the Matsubara weighting function will lead to identical results.
Table of Matsubara Frequency Summations
The following table concludes the Matsubara frequency summations for some simple rational functions g(z).
- .
η=±1 marks the statistical sign.
| [1] | |
| [2] | |
| [2] | |
[1] Since the summation does not converge, the result may differ by a constant upon different choice of the Matsubara weighting function.
[2] (1↔2) denotes the same expression as the before but with index 1 and 2 interchanged.
Applications in Physics
Zero Temperature Limit
In this limit , the Matsubara frequency summation is equivalent to the integration of imaginary frequency over imaginary axis.
- .
Some of the integrals do not converge. They should be regularized by introducing the frequency cutoff , and then subtracting the divergent part (-dependent) from the integral before taking the limit of . For example, the free energy is obtained by the integral of logarithm,
meaning that at zero temperature, the free energy simply relates to the internal energy below the chemical potential. Also the distribution function is obtained by the following integral
which shows step function behavior at zero temperature.
Green's Function Related
Time Domain
Consider a function G(τ) defined on the imaginary time interval (0,β). It can be given in terms of Fourier series,
,
where the frequency only takes discrete values spaced by 2π/β.
The particular choice of frequency depends on the boundary condition of the function G(τ). In physics, G(τ) stands for the imaginary time representation of Green's function
.
It satisfies periodic boundary condition G(τ+β)=G(τ) for boson field. While for fermion field the boundary condition is anti-periodic G(τ+β)=-G(τ).
Given the Green's function G(iω) in the frequency domain, its imaginary time representation G(τ) can be evaluated by Matsubara frequency summation. Depending on the boson or fermion frequencies that is to be summed over, the resulting G(τ) can be different. To distinguish, define
- ,
with
- ,
- .
Note that τ is restricted in the principal interval (0,β). The boundary condition can be used to extend G(τ) out of the principal interval. Some frequently used results are concluded in the following table.
Operator Switching Effect
The small imaginary time plays a critical role here. The order of the operators will change if the small imaginary time changes sign.
- .
Distribution Function
The evaluation of distribution function becomes tricky because of the discontinuity of Green's function G(τ) at τ=0. To evaluate the summation
- ,
both choices of the weighting function are acceptable, but the results are different. This can be understood if we push G(τ) away from τ=0 a little bit, then to control the convergence, we must take as the weighting function for , and for .
Bosons
- ,
- .
Fermions
- ,
- .
Free Energy
Bosons
- ,
Fermions
- .
Diagrams Evaluation
Frequently encountered diagrams are evaluated here with the single mode setting. Multiple modes problem can be approached by spectral function integral.
Fermion Self Energy
- .
Particle-Hole Bubble
- .
Particle-Particle Bubble
Appendix: Properties of Distribution Functions
Distribution Functions
The general notation stands for either Bose (η=+1) or Fermi (η=-1) distribution function
- .
If necessary, the specific notations nB and nF are used to indicate Bose and Fermi distribution functions respectively
- .
Relation to hyperbolic functions
The Bose distribution function is related to hyperbolic cotangent function by
- .
The Fermi distribution function is related to hyperbolic tangent function by
- .
Parity
Both distribution functions do not have definite parity,
- .
Another formula is in terms of the function
- .
However their derivatives have definite parity.
Bose-Fermi Transmutation
Bose and Fermi distribution functions transmute under a shift of the variable by the fermionic frequency,
- .
However shifting by bosonic frequencies does not make any difference.
Derivatives
First order
- ,
- .
In terms of product:
- .
In the zero temperature limit:
- as .
Second order
- ,
- .
Formula of difference
- .
Case a=0
- ,
- .
Case a→0
- ,
- .
Case b→0
- ,
- .
The function cη
Definition:
- .
For Bose and Fermi type:
- ,
- .
Relation to hyperbolic functions
- .
It is obvious that is positive definite.
To avoid overflow in the numerical calculation, the tanh and coth functions are used
- ,
- .
Case a=0
- ,
- .
Case b=0
- ,
- .
Low temperature limit
For a=0: .
For b=0: .
In general,
See also
External links
- Agustin Nieto: Evaluating Sums over the Matsubara Frequencies. arXiv:hep-ph/9311210
- Github repository: MatsubaraSum A Mathematica package for Matsubara frequency summation.
References
- ↑ A. Abrikosov, L. Gor'kov, I. Dzyaloshinskii: Methods of Quantum Field Theory in Statistical Physics., New York, Dover Publ., 1975, ISBN 0-486-63228-8