Induction of regular languages
In computational learning theory, induction of regular languages refers to the task of learning a formal description (e.g. grammar) of a regular language from a given set of example strings. Although Mark E. Gold has shown that not every regular language can be learned this way (see language identification in the limit), approaches have been investigated for a variety of subclasses. They are sketched in this article. For learning of more general grammars, see Grammar induction.
Example
A regular language is defined as a (finite or infinite) set of strings that can be described by one of the mathematical formalisms called "finite automaton", "regular grammar", or "regular expression", all of which have the same expressive power. Since the latter formalism leads to shortest notations, it shall be introduced and used here. Given a set Σ of symbols (a.k.a. alphabet), a regular expression can be any of
- ∅ (denoting the empty set of strings),
- ε (denoting the singleton set containing just the empty string),
- a (where a is any character in Σ; denoting the singleton set just containing the single-character string a),
- r+s (where r and s are, in turn, simpler regular expressions; denoting their set's union)
- r⋅s (denoting the set of all possible concatenations of strings from r 's and s 's set),
- r+ (denoting the set of n-fold repetitions of strings from r 's set, for any n≥1), or
- r* (similarly denoting the set of n-fold repetitions, but also including the empty string, seen as 0-fold repetition).
For example, using Σ = { 0,1 }, the regular expression (0+1+ε)⋅(0+1) denotes the set of all binary numbers with one or two digits (leading zero allowed), while 1⋅(0+1)*⋅0 denotes the (infinite) set of all even binary numbers (no leading zeroes).
Given a set of strings (also called "positive examples"), the task of regular language induction is to come up with a regular expression that denotes a set containing all of them. As an example, given { 1, 10, 100 }, a "natural" description could be the regular expression 1⋅0*, corresponding to the informal characterization "a 1 followed by arbitrarily many (maybe even none) 0es". However, (0+1)* and 1+(1⋅0)+(1⋅0⋅0) is another regular expression, denoting the largest (assuming Σ={0,1}) and the smallest set containing the given strings, and called the trivial overgeneralization and undergeneralization, respectively. Some approaches work in an extended setting where also a set of "negative example" strings is given; then, a regular expression is to be found that generates all of the positive, but none of the negative examples.
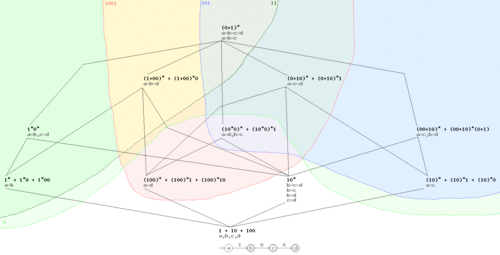 Lattice of automata generating the strings 1, 10, and 100 (positive examples). For each of the negative example strings 11, 1001, 101, and 0, the upper set of automata generating it is shown. The only automata that generate all of { 1, 10, 100 }, but none of { 11, 1001, 101, 0 } are the trivial bottom automaton and the one corresponding to the regular expression 1⋅0*. |
Lattice of automata
Dupont et al. have shown that the set of all structurally complete finite automata[note 1] generating a given input set of example strings forms a lattice, with the trivial undergeneralized and the trivial overgeneralized automaton as bottom and top element, respectively. Each member of this lattice can be obtained by factoring the undergeneralized automaton by an appropriate congruence relation. The image shows an example for the above input string set { 1, 10, 100 }. Each automaton is denoted by an equivalent regular expression. For the trivial undergeneralization at the bottom node, also the automaton form is sketched in grey, consisting of states a, b, c, and d. Each node's automaton is the result of factoring the bottom automaton by the congruence relation shown in grey below the node.
If both positive and negative example strings are given, Dupont et al. build the lattice from the positive examples, and then investigate the separation border between automata that generate some negative example and such that do not. Most interesting are those automata immediately below the border.[1] In the image, separation borders are shown for the negative example strings 11, 1001, 101, 0.
Coste and Nicolas present an own search method within this lattice, which they relate to Mitchell's version space paradigm. To find the separation border, they use a graph coloring algorithm on the state inequality relation induced by the negative examples.[2] Later, they investigate several ordering relations on the set of all possible state fusions.[3]
Kudo and Shimbo use the representation by automaton factorizations to give a unique framework for the following approaches (sketched below):
- k-reversible languages and the "tail clustering" follow-up approach,
- Successor automata and the predecessor-successor method, and
- pumping-based approaches (framework-integration challenged by Luzeaux,[4] however).
Each of these approaches is shown to correspond to a particular kind of congruence relations used for factorization.[5]
Approaches
k-reversible languages
Angluin considers so-called "k-reversible" regular automata, that is, deterministic automata in which each state can be reached from at most one state by following a transition chain of length k. Formally, if Σ, Q, and δ denote the input alphabet, the state set, and the transition function of an automaton A, respectively, then A is called k-reversible if : ∀a0,...,ak ∈ Σ ∀s1, s2 ∈ Q: δ*(s1,a0...ak) = δ*(s2,a0...ak) ⇒ s1 = s2, where δ* means the homomorphic extension of δ to arbitrary words. Angluin gives a cubic algorithm for learning of the smallest k-reversible language from a given set of input words; for k=0, the algorithm has even almost linear complexity.[6][7] The required state uniqueness after k+1 given symbols forces unifying automaton states, thus leading to a proper generalization different from the trivial undergeneralized automaton. This algorithm has been used to learn simple parts of English syntax;[8] later, an incremental version has been provided.[9] Another approach based on k-reversible automata is the tail clustering method.[10]
Successor automata
From a given set of input strings, Vernadat and Richetin build a so-called successor automaton, consisting of one state for each distinct character and a transition between each two adjacent characters' states.[11] For example, the singleton input set { aabbaabb } leads to an automaton corresponding to the regular expression (a+⋅b+)*.
An extension of this approach is the predecessor-successor method which generalizes each character repetition immediately to a Kleene + and then includes for each character the set of its possible predecessors in its state. Successor automata can learn exactly the class of local languages. Since each regular language is the homomorphic image of a local language, grammars from the former class can be learned by lifting, if an appropriate (depending on the intended application) homomorphism is provided. In particular, there is such a homomorphism for the class of languages learnable by the predecessor-successor method.[12] The learnability of local languages can be reduced to that of k-reversible languages.[13][14]
 Brzozowski derivative (on red background) of a dictionary string set with respect to "con" |
 Illustration of the pumping lemma for regular automata |
Early approaches
Chomsky and Miller (1957)[15] used the pumping lemma: they guess a part v of an input string uvw and try to build a corresponding cycle into the automaton to be learned; using membership queries they ask, for appropriate k, which of the strings uw, uvvw, uvvvw, ..., uvkw also belongs to the language to be learned, thereby refining the structure of their automaton. In 1959, Solomonoff generalized this approach to context-free languages, which also obey a pumping lemma.[16]
Cover automata
Câmpeanu et al. learn a finite automaton as a compact representation of a large finite language. Given such a language F, they search a so-called cover automaton A such that its language L(A) covers F in the following sense: L(A) ∩ Σ≤l = F, where l is the length of the longest string in F, and Σ≤l denotes the set of all strings not longer than l. If such a cover automaton exists, F is uniquely determined by A and l. For example, F = { ad, read, reread } has l=6 and a cover automaton corresponding to the regular expression (r⋅e)*⋅a⋅d.
For two strings x and y, Câmpeanu et al. define x ~ y if xz∈F ⇔ yz∈F for all strings z of a length such that both xz and yz are not longer than l.[17] Based on this relation, whose lack of transitivity[note 2] causes considerable technical problems, they give an O(n4)[note 3] algorithm to construct from F a cover automaton A of minimal state count. Moreover, for union, intersection, and difference of two finite languages they provide corresponding operations on their cover automata.[18][19] Păun et al. improve the time complexity to O(n2).[20]
Residual automata
For a set S of strings and a string u, the Brzozowski derivative u−1S is defined as the set of all rest-strings obtainable from a string in S by cutting off its prefix u (if possible), formally: u−1S = { v ∈ Σ*: uv ∈ S }, cf. picture.[21] Denis et al. define a residual automaton to be a nondeterministic finite automaton A where each state q corresponds to a Brzozowski derivative of its accepted language L(A), formally: ∀q∈Q ∃u∈Σ*: L(A,q) = u−1L(A), where L(A,q) denotes the language accepted from q as start state.
They show that each regular language is generated by a uniquely determined minimal residual automaton. Its states are ∪-indecomposable Brzozowski derivatives, and it may be exponentially smaller than the minimal deterministic automaton. Moreover, they show that residual automata for regular languages cannot be learned in polynomial time, even assuming optimal sample inputs. They give a learning algorithm for residual automata and prove that it learns the automaton from its characteristic sample of positive and negative input strings.[22][23]
Reduced regular expressions
Brill defines a reduced regular expression to be any of
- a (where a is any character in Σ; denoting the singleton set just containing the single-character string a),
- ¬a (denoting any other single character in Σ except a),
- • (denoting any single character in Σ)
- a*, (¬a)*, or •* (denoting arbitrarily many, possibly zero, repetitions of characters from the set of a, ¬a, or •, respectively), or
- r⋅s (where r and s are, in turn, simpler reduced regular expressions; denoting the set of all possible concatenations of strings from r 's and s 's set).
Given an input set of strings, he builds step by step a tree with each branch labelled by a reduced regular expression accepting a prefix of some input strings, and each node labelled with the set of lengths of accepted prefixes. He aims at learning correction rules for English spelling errors,[note 4] rather than at theoretical considerations about learnability of language classes. Consequently, he uses heuristics to prune the tree-buildup, leading to a considerable improvement in run time.[24]
Applications
- Finding common patterns in DNA and RNA structure descriptions [25][26] (Bioinformatics)
- Modelling natural language acquisition by humans [27]
- Learning of structural descriptions from structured example documents, in particular Document Type Definitions (DTD) from SGML documents [28]
- Learning the structure of music pieces [29][30]
- Obtaining compact representations of finite languages [18]
- Classifying and retrieving documents [31]
- Generating of context-dependent correction rules for English grammatical errors [24]
Notes
- ↑ i.e. finite automata without unnecessary states and transitions, with respect to the given input set of strings
- ↑ For example, F = { aab, baa, aabb } leads to aab ~ aabb (only z=ε needs to be considered to check this) and aabb ~ baa (similarly), but not aab ~ baa (due to the case z=b). According to Câmpeanu et al. (2001, Lemma 1, p.5), however x ~ y ∧ y ~ z → x ~ z holds for strings x, y, z with |x| ≤ |y| ≤ |z|.
- ↑ where n is the number of states of a DFA AF such that L(AF) = F
- ↑ For example: Replace "past" by "passed" in the context "(¬t⋅o)*⋅SINGULAR_NOUN⋅past"
References
- ↑ P. Dupont; L. Miclet; E. Vidal (1994). "What is the Search Space of the Regular Inference?". In R. C. Carrasco; J. Oncina. Proceedings of the Second International Colloquium on Grammatical Inference (ICGI): Grammatical Inference and Applications. LNCS. 862. Springer. pp. 25–37.
- ↑ F. Coste; J. Nicolas (1997). "Regular Inference as a Graph Coloring Problem". Proc. ICML Workshop on Grammatical Inference, Automata Induction, and Language Acquisition.
- ↑ F. Coste; J. Nicolas (1998). "How Considering Incompatible State Mergings May Reduce the DFA Induction Search Tree". In Vasant Honavar; Giora Slutzki. Grammatical Inference, 4th International Colloquium, ICGI. LNCS. 1433. Springer. pp. 199–210.
- ↑ Dominique Luzeaux (Aug 1997). "A Universal Approach to Positive Regular Grammar Inference". Proc. 15th World IMACS Congress on Scientific Computation, Modelling and Applied Mathematics.
- ↑ M. Kudo; M. Shimbo (1988). "Efficient Regular Grammatical Inference Techniques by the Use of Partial Similarities and Their Logical Relationships". Pattern Recognition. 21: 401–409. doi:10.1016/0031-3203(88)90053-2.
- ↑ D. Angluin (1981). "A Note on the Number of Queries Needed to Identify Regular Languages". Information and Control. 51: 76–87. doi:10.1016/s0019-9958(81)90090-5.
- ↑ D. Angluin (1982). "Inference of Reversible Languages". J.ACM. 293: 741–765.
- ↑ Robert C. Berwick; Samuel F. Pilato (1987). "Learning Syntax by Automata Induction". Machine Learning. 2 (1): 9–38. doi:10.1007/bf00058753.
- ↑ Rajesh Parekh; Codrin Nichitiu; Vasant Honavar (Jan 1997). A Polynomial Time Incremental Algorithm for Regular Grammar Inference (Technical report). AI Research Group, Iowa State Univ. p. 14. TR 97-03.
- ↑ L. Miclet; C. Faure (1985). Reconnaissance des Formes Structurelle: Développement et Tendances (Technical report). INRIA.
- ↑ F. Vernadat; M. Richetin (1984). "Regular Inference for Syntactic Pattern Recognition: A Case Study". Proc. 7th International Conference on Pattern Recognition (ICPR). pp. 1370–1372.
- ↑ P. Garcia; E. Vidal; F. Casacuberta (1987). "Local Languages, The Successor Method, and a Step Towards a General Methodology for the Inference of Regular Grammars". IEEE Trans. on Pattern Analysis and Machine Intelligence. 9.
- ↑ Takashi Yokomori (Oct 1989). "Learning Context-Free Languages Efficiently". In K.P. Jantke. Proc. Int. Workshop AII. LNAI. 397. Springer. pp. 104–123.
- ↑ Satoshi Kobayashi; Takashi Yokomori (1994). "Learning Concatenations of Locally Testable Languages from Positive Data". In Setsuo Arikawa; Klaus P. Jantke. Proc. 5th ALT. LNAI. 872. Springer. pp. 405–422.
- ↑ N. Chomsky; G.A. Miller (1957). Pattern Conception (Technical report). ASTIA. Document AD110076.
- ↑ R. Solomonoff (Jun 1959). "A New Method for Discovering the Grammars of Phrase Structure Languages". Proc. Int. Conf. on Information Processing. R.Oldenbourg. pp. 285–290.
- ↑ This relation generalizes the relation RF from the Myhill-Nerode theorem. It has been investigated in more detail in sect.3 of: Cynthia Dwork; Larry Stockmeyer (1990). "A Time Complexity Gap for Two-Way Probabilistic Finite-State Automata". SIAM Journal on Computing. 19 (6): 1011–1023. doi:10.1137/0219069.
- 1 2 Cezar Câmpeanu; Nicolae Sântean; Sheng Yu (1998). "Minimal Cover-Automata for Finite Languages". In J.-M. Champarnaud; D. Maurel; D. Ziadi. Proc. Workshop on Implementing Automata (WIA) (PDF). LNCS. 1660. Springer. pp. 43–56. doi:10.1007/3-540-48057-9_4.
- ↑ Cezar Câmpeanu; Nicolae Sântean; Sheng Yu (2001). "Minimal Cover-Automata for Finite Languages" (PDF). Theoretical Computer Science. 267: 3–16. doi:10.1016/s0304-3975(00)00292-9.
- ↑ Andrei Păun; Nicolae Sântean; Sheng Yu (Sep 2001). "An O(n2) Algorithm for Constructing Minimal Cover Automata for Finite Languages". In Sheng Yu; Andrei Păun. Proc. 5th Int. Conf. on Implementation and Application of Automata (CIAA) (PDF). LNCS. 2088. Springer. pp. 243–251. ISBN 978-3-540-42491-8.
- ↑ Janusz A. Brzozowski (1964). "Derivatives of Regular Expressions". JACM. 11: 481–494. doi:10.1145/321239.321249.
- ↑ François Denis; Aurélien Lemay; Alain Terlutte (2000). "Learning Regular Languages Using Non Deterministic Finite Automata". In Arlindo L. Oliveira. Grammatical Inference: Algorithms and Applications, 5th International Colloquium, ICGI. LNCS. 1891. Springer. pp. 39–50. ISBN 3-540-41011-2.
- ↑ François Denis; Aurélien Lemay; Alain Terlutte (2001). "Learning Regular Languages using RFSA". Proc. ALT '01 (PDF).
- 1 2 Eric Brill (2000). "Pattern–Based Disambiguation for Natural Language Processing". Proc. EMNLP/VLC.
- ↑ Alvis Brazma; Inge Jonassen; Jaak Vilo; Esko Ukkonen (1998). "Pattern Discovery in Biosequences". In Vasant Honavar; Giora Slutzki. Grammatical Inference, 4th International Colloquium, ICGI. LNCS. 1433. Springer. pp. 257–270.
- ↑ M.S. Waterman, ed. (Jan 1989). Mathematical Methods for DNA Sequences. CRC Press. ISBN 084936664X.
- ↑ Fernando Pereira; Yves Schabes (1992). "Inside-Outside Reestimation for partially Bracketed Corpora". Proc. 30th Ann. Meeting of the Assoc. for Comp. Linguistics. pp. 128–135.
- ↑ Helena Ahonen (Nov 1996). Generating Grammars for Structured Documents Using Grammatical Inference Methods (Ph.D.). Report. A-1996-4. University of Helsinki, Department of Computer Science.
- ↑ Stephen Watkinson (1997). Induction of Musical Syntax (Master). Dept. of AI, Univ. Edinburgh. Archived from the original on June 4, 2001.
- ↑ Pedro P. Cruz-Alcázar; Enrique Vidal (1998). "Learning Regular Grammars to Model Musical Style: Comparing Different Coding Schemes". In Vasant Honavar; Giora Slutzki. Grammatical Inference, 4th International Colloquium, ICGI. LNCS. 1433. Springer. pp. 211–222.
- ↑ Alexander S. Saidi; Souad Tayeb-bey (1998). "Grammatical Inference in Document Recognition". In Vasant Honavar; Giora Slutzki. Grammatical Inference, 4th International Colloquium, ICGI. LNCS. 1433. Springer. pp. 175–186. ISBN 3-540-64776-7.