Gnomonic projection

A gnomonic map projection displays all great circles as straight lines, resulting in any straight line segment on a gnomonic map showing a geodesic, the shortest route between the segment's two endpoints. This is achieved by casting surface points of the sphere onto a tangent plane, each landing where a ray from the center of the sphere passes through the point on the surface and then on to the plane. No distortion occurs at the tangent point, but distortion increases rapidly away from it. Less than half of the sphere can be projected onto a finite map. Consequently, a rectilinear photographic lens, which is based on the gnomonic principle, cannot image more than 180 degrees.
History
The gnomonic projection is said to be the oldest map projection, developed by Thales in the 6th century BC. The path of the shadow-tip or light-spot in a nodus-based sundial traces out the same hyperbolae formed by parallels on a gnomonic map.
Properties
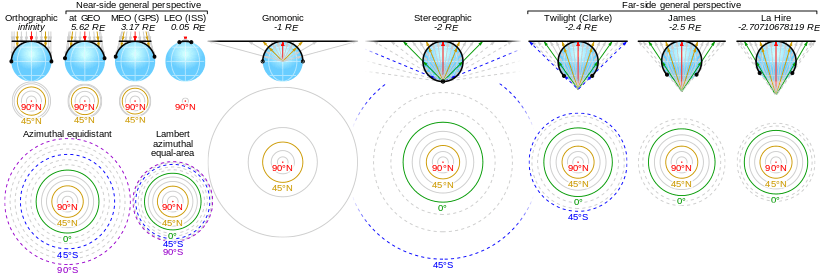
Since meridians and the equator are great circles, they are always shown as straight lines on a gnomonic map.
- If the tangent point is one of the poles then the meridians are radial and equally spaced. The equator is at infinity in all directions. Other parallels are depicted as concentric circles.
- If the tangent point is not on a pole or the equator, then the meridians are radially outward straight lines from a Pole, but not equally spaced. The equator is a straight line that is perpendicular to only one meridian, indicating that the projection is not conformal. Other parallels are depicted as conic sections.
- If the tangent point is on the equator then the meridians are parallel but not equally spaced. The equator is a straight line perpendicular to the meridians. Other parallels are depicted as hyperbolae.

As with all azimuthal projections, angles from the tangent point are preserved. The map distance from that point is a function r(d) of the true distance d, given by
where R is the radius of the Earth. The radial scale is
and the transverse scale
so the transverse scale increases outwardly, and the radial scale even more.
Use
Gnomonic projections are used in seismic work because seismic waves tend to travel along great circles. They are also used by navies in plotting direction finding bearings, since radio signals travel along great circles. Meteors also travel along great circles, with the Gnomonic Atlas Brno 2000.0 being the IMO's recommended set of star charts for visual meteor observations. Aircraft and ship pilots use the projection to find the shortest route between start and destination.
The gnomonic projection is used extensively in photography, where it is called rectilinear projection.
The gnomonic projection is used in astronomy where the tangent point is centered on the object of interest. The sphere being projected in this case is the celestial sphere, R = 1, and not the surface of the Earth.
See also
- List of map projections
- Beltrami–Klein model, the analogous mapping of the hyperbolic plane
References
- Snyder, John P. (1987). Map Projections - A Working Manual. U.S. Geological Survey Professional Paper 1395. United States Government Printing Office, Washington, D.C. This paper can be downloaded from USGS pages
- Calabretta, M. R.; Greisen, E. W. (2002). "Representations of celestial coordinates in FITS (Paper II)". Astronomy & Astrophysics. 395. pp. 1077–1122.
External links
| Wikimedia Commons has media related to Gnomonic projection. |
- http://www.bfi.org/node/25 Description of the Fuller Projection map from the Buckminster Fuller Institute
- http://erg.usgs.gov/isb/pubs/MapProjections/projections.html#gnomonic Explanations of projections by USGS
- http://exchange.manifold.net/manifold/manuals/6_userman/mfd50Gnomonic.htm
- Gnomonic Projection
- The Gnomonic Projection
- Table of examples and properties of all common projections, from radicalcartography.net
- Sphaerica geometry software, is capable of displaying spherical geometry constructions in gnomonic projection