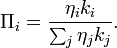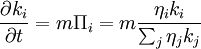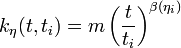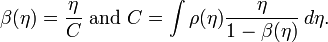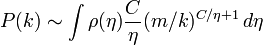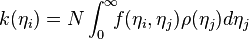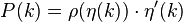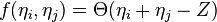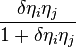Fitness model (network theory)
In complex network theory, the fitness model is a model of the evolution of a network: how the links between nodes change over time depends on the fitness of nodes. Fitter nodes attract more links at the expense of less fit nodes.
It has been used to model the network structure of the World Wide Web.
Description of the model
The model is based on the idea of fitness, an inherent competitive factor that nodes may have, capable of affecting the network's evolution.[1] According to this idea, the nodes' intrinsic ability to attract links in the network varies from node to node, the most efficient (or "fit") being able to gather more edges in the expense of others. In that sense, not all nodes are identical to each other, and they claim their degree increase according to the fitness they possess every time. The fitness factors of all the nodes composing the network may form a distribution ρ(η) characteristic of the system been studied.
Bianconi and Barabási[2] proposed a new model called Bianconi-Barabasi model, a variant to the Barabási-Albert model (BA model), where the probability for a node to connect to another one is supplied with a term expressing the fitness of the node involved. The fitness parameter is time independent and is multiplicative to the probability
Thus, the system of equations for the time evolution of the degrees 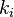 according to the continuum theory introduced by the same model will have the form
according to the continuum theory introduced by the same model will have the form
where m the number of edges the newly coming node has. If we require the solution to have a similar form to the one it had without the insertion of the fitness factors (to avoid ruining the power-law degree distribution of scale-free networks), then the exponent of the solution has to change and become fitness dependent
where
Hence, the more fit nodes increase their degree faster than the less ones. This characteristic attributes the network with a different behavior regarding its evolution. Without the introduction of the fitness property, all nodes had the same exponent in the power-law degree evolution formula. This means that the older nodes in the system would have more edges compared to newcoming ones. After the fitness property is introduced, this exponent, and accordingly, the slope of 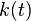 change, giving thus the opportunity to newcoming nodes to dominate the system.
change, giving thus the opportunity to newcoming nodes to dominate the system.
It was seen through this example how can a network's evolution change behavior through the introduction of a new parameter in the model. However, we require the network to preserve its overall scale-free character. By forcing the fitness dependence to be accumulated in the exponent only, the degree-distribution will still be a power-law relationship, composed though by a weighted sum of different power-law in degree-evolution formulas
where 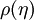 is the fitness distribution depending on the system's composition
is the fitness distribution depending on the system's composition
The fitness model can be extended to in corporate additional processes, such as internal edges, which affect the exponents.[3]
Another model where the fitness is not coupled to preferential attachment has been introduced by Caldarelli et al.[4] Here a link is created between two vertices 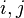 with a probability given by a linking function
with a probability given by a linking function 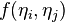 of the fitnesses of the vertices involved.
The degree of a vertex i is given by [5]
of the fitnesses of the vertices involved.
The degree of a vertex i is given by [5]
If 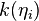 is an invertible and increasing function of
is an invertible and increasing function of 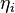 , then
the probability distribution
, then
the probability distribution 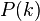 is given by
is given by
As a result if the fitnesses 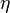 are distributed as a power law, then also the node degree does.
are distributed as a power law, then also the node degree does.
Less intuitively with a fast decaying probability distribution as
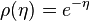 together with a linking function of the kind
together with a linking function of the kind
with 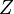 a constant and
a constant and 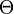 the Heavyside function, we also obtain
scale-free networks.
the Heavyside function, we also obtain
scale-free networks.
Such model has been successfully applied to describe trade between nations by using GDP as fitness for the various nodes 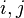 and a linking function of the kind
[6]
[7]
and a linking function of the kind
[6]
[7]
Fitness model and the evolution of the Web
The fitness model has been used to model the network structure of the World Wide Web. In a PNAS article,[8] Kong et al. extended the fitness model to include random node deletion, a common phenomena in the Web. When the deletion rate of the web pages are accounted for, they found that the overall fitness distribution is exponential. Nonetheless, even this small variance in the fitness is amplified through the preferential attachment mechanism, leading to a heavy-tailed distribution of incoming links on the Web.
See also
References
- ↑ Albert R. and Barabási A.-L., "Statistical mechanics of complex networks", Reviews of Modern Physics 74, 47 (2002)
- ↑ Bianconi Ginestra and Barabási A.-L., 2001a, Europhys. Lett. 54, 436.
- ↑ Ergun, G. and G. J. Rodgers, Physica A 303 (2002) 261–272
- ↑ Caldarelli G., A. Capocci, P. De Los Rios, M.A. Muñoz, Physical Review Letters 89, 258702 (2002)
- ↑ Servedio V.D.P., G. Caldarelli, P. Buttà, Physical Review E 70, 056126 (2004)
- ↑ Garlaschelli D., M I Loffredo Physical Review Letters 93, 188701 (2004)
- ↑ Cimini G., T. Squartini, D. Garlaschelli and A. Gabrielli, Scientific Reports 5, 15758 (2015)
- ↑ J.S. Kong, N. Sarshar, V.P. Roychowdhury, "Experience versus Talent Shapes the Structure of the Web", Proceedings of the National Academy of Sciences of the USA, September 16, 2008; 105 (37)