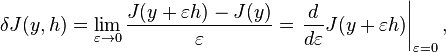First variation

In applied mathematics and the calculus of variations, the first variation of a functional J(y) is defined as the linear functional 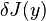\delta J(y) mapping the function h to

\delta J(y,h) = \lim_{\varepsilon\to 0} \frac{J(y + \varepsilon h)-J(y)}{\varepsilon} = \left.\frac{d}{d\varepsilon} J(y + \varepsilon h)\right|_{\varepsilon = 0},

where y and h are functions, and ε is a scalar. This is recognizable as the Gâteaux derivative of the functional.

Example

Compute the first variation of

J(y)=\int_a^b yy' dx.

From the definition above,

\begin{align} \delta J(y,h)&=\left.\frac{d}{d\varepsilon} J(y + \varepsilon h)\right|_{\varepsilon = 0}\\ &= \left.\frac{d}{d\varepsilon} \int_a^b (y + \varepsilon h)(y^\prime + \varepsilon h^\prime) \ dx\right|_{\varepsilon = 0}\\ &= \left.\frac{d}{d\varepsilon} \int_a^b (yy^\prime + y\varepsilon h^\prime + y^\prime\varepsilon h + \varepsilon^2 hh^\prime) \ dx\right|_{\varepsilon = 0}\\ &= \left.\int_a^b \frac{d}{d\varepsilon} (yy^\prime + y\varepsilon h^\prime + y^\prime\varepsilon h + \varepsilon^2 hh^\prime) \ dx\right|_{\varepsilon = 0}\\ &= \left.\int_a^b (yh^\prime + y^\prime h + 2\varepsilon hh^\prime) \ dx\right|_{\varepsilon = 0}\\ &= \int_a^b (yh^\prime + y^\prime h) \ dx \end{align}

See also

External links


This article is issued from Wikipedia - version of the 9/3/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.