Finite strain theory

Laws

Conservations
Energy Mass Momentum
Inequalities
Clausius–Duhem (entropy)

Solid mechanics

Contact mechanics (frictional)

Fluid mechanics

Fluids
Statics · Dynamics Archimedes' principle · Bernoulli's principle Navier–Stokes equations Poiseuille equation · Pascal's law Viscosity (Newtonian · non-Newtonian) Buoyancy · Mixing · Pressure
Liquids
Surface tension Capillary action
Gases
Atmosphere Boyle's law Charles's law Gay-Lussac's law Combined gas law
Plasma

Rheology

Smart fluids
Viscoelasticity Rheometry Rheometer
Magnetorheological Electrorheological Ferrofluids

Scientists

In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which both rotations and strains are arbitrarily large, i.e. invalidates the assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of the continuum are significantly different and a clear distinction has to be made between them. This is commonly the case with elastomers, plastically-deforming materials and other fluids and biological soft tissue.

Displacement

Figure 1. Motion of a continuum body.

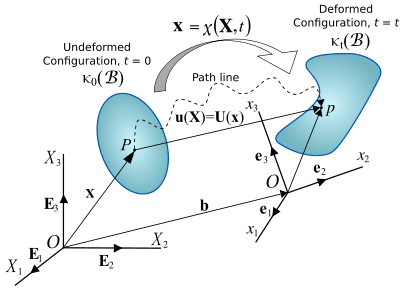
The displacement of a body has two components: a rigid-body displacement and a deformation.

A rigid-body displacement consists of a simultaneous translation and rotation of the body without changing its shape or size.
Deformation implies the change in shape and/or size of the body from an initial or undeformed configuration $\kappa _{0}({\mathcal B})\,\!$ to a current or deformed configuration $\kappa _{t}({\mathcal B})\,\!$ (Figure 1).

A change in the configuration of a continuum body can be described by a displacement field. A displacement field is a vector field of all displacement vectors for all particles in the body, which relates the deformed configuration with the undeformed configuration. Relative displacement between particles occurs if and only if deformation has occurred. If displacement occurs without deformation, then it is deemed a rigid-body displacement.

Material coordinates (Lagrangian description)

The displacement of particles indexed by variable $i$ may be expressed as follows. The vector joining the positions of a particle in the undeformed configuration $P_{i}\,\!$ and deformed configuration $p_{i}\,\!$ is called the displacement vector. Using ${\mathbf {X}}\,\!$ in place of $P_{i}\,\!$ and ${\mathbf {x}}\,\!$ in place of $p_{i}\,\!$ , both of which are vectors from the origin of the coordinate system to each respective point, we have the Lagrangian description of the displacement vector:

{\mathbf u}({\mathbf X},t)=u_{i}{\mathbf e}_{i}\,\!

Where ${\mathbf e}_{i}\,\!$ is the unit vector that defines the basis of the spatial (lab-frame) coordinate system.

Expressed in terms of the material coordinates, the displacement field is:

{\mathbf u}({\mathbf X},t)={\mathbf b}(t)+{\mathbf x}({\mathbf X},t)-{\mathbf X}\qquad {\text{or}}\qquad u_{i}=\alpha _{{iJ}}b_{J}+x_{i}-\alpha _{{iJ}}X_{J}\,\!

Where $\mathbf {b} (t)$ is the displacement vector representing rigid-body translation.

The partial derivative of the displacement vector with respect to the spatial coordinates yields the material displacement gradient tensor $\nabla _{{{\mathbf X}}}{\mathbf u}\,\!$ . Thus we have,

{\begin{aligned}\nabla _{{{\mathbf X}}}{\mathbf u}&=\nabla _{{{\mathbf X}}}{\mathbf x}-{\mathbf I}={\mathbf F}-{\mathbf I}\qquad &{\text{or}}&\qquad {\frac {\partial u_{i}}{\partial X_{K}}}={\frac {\partial x_{i}}{\partial X_{K}}}-\delta _{{iK}}=F_{{iK}}-\delta _{{iK}}\end{aligned}}

where ${\mathbf F}\,\!$ is the deformation gradient tensor.

Spatial coordinates (Eulerian description)

In the Eulerian description, the vector joining the positions of a particle $P\,\!$ in the undeformed configuration and deformed configuration is called the displacement vector:

\mathbf {U} (\mathbf {x} ,t)=U_{J}\mathbf {E} _{J}\,\!

Where ${\mathbf E}_{i}\,\!$ is the unit vector that defines the basis of the material (body-frame) coordinate system.

Expressed in terms of spatial coordinates, the displacement field is:

{\mathbf U}({\mathbf x},t)={\mathbf b}(t)+{\mathbf x}-{\mathbf X}({\mathbf x},t)\qquad {\text{or}}\qquad U_{J}=b_{J}+\alpha _{{Ji}}x_{i}-X_{J}\,\!

The partial derivative of the displacement vector with respect to the material coordinates yields the spatial displacement gradient tensor $\nabla _{{{\mathbf x}}}{\mathbf U}\,\!$ . Thus we have,

{\begin{aligned}\nabla _{{{\mathbf x}}}{\mathbf U}&={\mathbf I}-\nabla _{{{\mathbf x}}}{\mathbf X}={\mathbf I}-{\mathbf F}^{{-1}}\qquad &{\text{or}}&\qquad {\frac {\partial U_{J}}{\partial x_{k}}}=\delta _{{Jk}}-{\frac {\partial X_{J}}{\partial x_{k}}}=\delta _{{Jk}}-F_{{Jk}}^{{-1}}\,.\end{aligned}}

Relationship between the material and spatial coordinate systems

$\alpha _{{Ji}}\,\!$ are the direction cosines between the material and spatial coordinate systems with unit vectors ${\mathbf E}_{J}\,\!$ and ${\mathbf e}_{i}\,\!$ , respectively. Thus

{\mathbf E}_{J}\cdot {\mathbf e}_{i}=\alpha _{{Ji}}=\alpha _{{iJ}}\,\!

The relationship between $u_{i}\,\!$ and $U_{J}\,\!$ is then given by

u_{i}=\alpha _{{iJ}}U_{J}\qquad {\text{or}}\qquad U_{J}=\alpha _{{Ji}}u_{i}\,\!

Knowing that

{\mathbf e}_{i}=\alpha _{{iJ}}{\mathbf E}_{J}\,\!

then

{\mathbf u}({\mathbf X},t)=u_{i}{\mathbf e}_{i}=u_{i}(\alpha _{{iJ}}{\mathbf E}_{J})=U_{J}{\mathbf E}_{J}={\mathbf U}({\mathbf x},t)\,\!

Combining the coordinate systems of deformed and undeformed configurations

It is common to superimpose the coordinate systems for the deformed and undeformed configurations, which results in ${\mathbf b}=0\,\!$ , and the direction cosines become Kronecker deltas, i.e.

{\mathbf E}_{J}\cdot {\mathbf e}_{i}=\delta _{{Ji}}=\delta _{{iJ}}\,\!

Thus in material (deformed) coordinates, the displacement may be expressed as:

{\mathbf u}({\mathbf X},t)={\mathbf x}({\mathbf X},t)-{\mathbf X}\qquad {\text{or}}\qquad u_{i}=x_{i}-\delta _{{iJ}}X_{J}\,\!

And in spatial (undeformed) coordinates, the displacement may be expressed as:

{\mathbf U}({\mathbf x},t)={\mathbf x}-{\mathbf X}({\mathbf x},t)\qquad {\text{or}}\qquad U_{J}=\delta _{{Ji}}x_{i}-X_{J}\,\!

Deformation gradient tensor

Figure 2. Deformation of a continuum body.

The deformation gradient tensor ${\mathbf F}({\mathbf X},t)=F_{{jK}}{\mathbf e}_{j}\otimes {\mathbf I}_{K}\,\!$ is related to both the reference and current configuration, as seen by the unit vectors ${\mathbf e}_{j}\,\!$ and ${\mathbf I}_{K}\,\!$ , therefore it is a two-point tensor.

Due to the assumption of continuity of $\chi ({\mathbf X},t)\,\!$ , ${\mathbf F}\,\!$ has the inverse ${\mathbf H}={\mathbf F}^{{-1}}\,\!$ , where ${\mathbf H}\,\!$ is the spatial deformation gradient tensor. Then, by the implicit function theorem,^[1] the Jacobian determinant $J({\mathbf X},t)\,\!$ must be nonsingular, i.e. $J({\mathbf X},t)=\det {\mathbf F}({\mathbf X},t)\neq 0\,\!$

The material deformation gradient tensor ${\mathbf F}({\mathbf X},t)=F_{{jK}}{\mathbf e}_{j}\otimes {\mathbf I}_{K}\,\!$ is a second-order tensor that represents the gradient of the mapping function or functional relation $\chi ({\mathbf X},t)\,\!$ , which describes the motion of a continuum. The material deformation gradient tensor characterizes the local deformation at a material point with position vector ${\mathbf X}\,\!$ , i.e. deformation at neighbouring points, by transforming (linear transformation) a material line element emanating from that point from the reference configuration to the current or deformed configuration, assuming continuity in the mapping function $\chi ({\mathbf X},t)\,\!$ , i.e. differentiable function of ${\mathbf {X}}\,\!$ and time $t\,\!$ , which implies that cracks and voids do not open or close during the deformation. Thus we have,

{\begin{aligned}d{\mathbf {x}}&={\frac {\partial {\mathbf {x}}}{\partial {\mathbf {X}}}}\,d{\mathbf {X}}\qquad &{\text{or}}&\qquad dx_{j}={\frac {\partial x_{j}}{\partial X_{K}}}\,dX_{K}\\&=\nabla \chi ({\mathbf X},t)\,d{\mathbf {X}}={\mathbf F}({\mathbf X},t)\,d{\mathbf {X}}\qquad &{\text{or}}&\qquad dx_{j}=F_{{jK}}\,dX_{K}\,.\end{aligned}}\,\!

Relative displacement vector

Consider a particle or material point $P\,\!$ with position vector ${\mathbf X}=X_{I}{\mathbf I}_{I}\,\!$ in the undeformed configuration (Figure 2). After a displacement of the body, the new position of the particle indicated by $p\,\!$ in the new configuration is given by the vector position ${\mathbf {x}}=x_{i}{\mathbf e}_{i}\,\!$ . The coordinate systems for the undeformed and deformed configuration can be superimposed for convenience.

Consider now a material point $Q\,\!$ neighboring $P\,\!$ , with position vector ${\mathbf {X}}+\Delta {\mathbf {X}}=(X_{I}+\Delta X_{I}){\mathbf I}_{I}\,\!$ . In the deformed configuration this particle has a new position $q\,\!$ given by the position vector ${\mathbf {x}}+\Delta {\mathbf {x}}\,\!$ . Assuming that the line segments $\Delta X\,\!$ and $\Delta {\mathbf x}\,\!$ joining the particles $P\,\!$ and $Q\,\!$ in both the undeformed and deformed configuration, respectively, to be very small, then we can express them as $d{\mathbf X}\,\!$ and $d{\mathbf x}\,\!$ . Thus from Figure 2 we have

{\begin{aligned}{\mathbf {x}}+d{\mathbf {x}}&={\mathbf {X}}+d{\mathbf {X}}+{\mathbf {u}}({\mathbf {X}}+d{\mathbf {X}})\\d{\mathbf {x}}&={\mathbf {X}}-{\mathbf {x}}+d{\mathbf {X}}+{\mathbf {u}}({\mathbf {X}}+d{\mathbf {X}})\\&=d{\mathbf {X}}+{\mathbf {u}}({\mathbf {X}}+d{\mathbf {X}})-{\mathbf {u}}({\mathbf {X}})\\&=d{\mathbf {X}}+d{\mathbf {u}}\\\end{aligned}}\,\!

where ${\mathbf {du}}\,\!$ is the relative displacement vector, which represents the relative displacement of $Q\,\!$ with respect to $P\,\!$ in the deformed configuration.

Taylor approximation

For an infinitesimal element $d{\mathbf X}\,\!$ , and assuming continuity on the displacement field, it is possible to use a Taylor series expansion around point $P\,\!$ , neglecting higher-order terms, to approximate the components of the relative displacement vector for the neighboring particle $Q\,\!$ as

{\begin{aligned}{\mathbf {u}}({\mathbf {X}}+d{\mathbf {X}})&={\mathbf {u}}({\mathbf {X}})+d{\mathbf {u}}\quad &{\text{or}}&\quad u_{i}^{*}=u_{i}+du_{i}\\&\approx {\mathbf {u}}({\mathbf {X}})+\nabla _{{{\mathbf X}}}{\mathbf u}\cdot d{\mathbf X}\quad &{\text{or}}&\quad u_{i}^{*}\approx u_{i}+{\frac {\partial u_{i}}{\partial X_{J}}}dX_{J}\,.\end{aligned}}\,\!

Thus, the previous equation $d{\mathbf x}=d{\mathbf {X}}+d{\mathbf {u}}\,\!$ can be written as

{\begin{aligned}d{\mathbf x}&=d{\mathbf X}+d{\mathbf u}\\&=d{\mathbf X}+\nabla _{{{\mathbf X}}}{\mathbf u}\cdot d{\mathbf X}\\&=\left({\mathbf I}+\nabla _{{{\mathbf X}}}{\mathbf u}\right)d{\mathbf X}\\&={\mathbf F}d{\mathbf X}\end{aligned}}\,\!

Time-derivative of the deformation gradient

Calculations that involve the time-dependent deformation of a body often require a time derivative of the deformation gradient to be calculated. A geometrically consistent definition of such a derivative requires an excursion into differential geometry^[2] but we avoid those issues in this article.

The time derivative of $\mathbf {F}$ is

{\dot {{\mathbf {F}}}}={\frac {\partial {\mathbf {F}}}{\partial t}}={\frac {\partial }{\partial t}}\left[{\frac {\partial {\mathbf {x}}({\mathbf {X}},t)}{\partial {\mathbf {X}}}}\right]={\frac {\partial }{\partial {\mathbf {X}}}}\left[{\frac {\partial {\mathbf {x}}({\mathbf {X}},t)}{\partial t}}\right]={\frac {\partial }{\partial {\mathbf {X}}}}\left[{\mathbf {V}}({\mathbf {X}},t)\right]

where $\mathbf {V}$ is the velocity. The derivative on the right hand side represents a material velocity gradient. It is common to convert that into a spatial gradient, i.e.,

{\dot {{\mathbf {F}}}}={\frac {\partial }{\partial {\mathbf {X}}}}\left[{\mathbf {V}}({\mathbf {X}},t)\right]={\frac {\partial }{\partial {\mathbf {x}}}}\left[{\mathbf {v}}({\mathbf {x}},t)\right]\cdot {\frac {\partial {\mathbf {x}}({\mathbf {X}},t)}{\partial {\mathbf {X}}}}={\boldsymbol {l}}\cdot {\mathbf {F}}

where ${\boldsymbol {l}}$ is the spatial velocity gradient. If the spatial velocity gradient is constant, the above equation can be solved exactly to give

{\mathbf {F}}=e^{{{\boldsymbol {l}}\,t}}

assuming ${\mathbf {F}}={\mathbf {1}}$ at $t=0$ . There are several methods of computing the exponential above.

Related quantities often used in continuum mechanics are the rate of deformation tensor and the spin tensor defined, respectively, as:

{\boldsymbol {d}}={\tfrac {1}{2}}\left({\boldsymbol {l}}+{\boldsymbol {l}}^{T}\right)\,,~~{\boldsymbol {w}}={\tfrac {1}{2}}\left({\boldsymbol {l}}-{\boldsymbol {l}}^{T}\right)\,.

The rate of deformation tensor gives the rate of stretching of line elements while the spin tensor indicates the rate of rotation or vorticity of the motion.

Transformation of a surface and volume element

To transform quantities that are defined with respect to areas in a deformed configuration to those relative to areas in a reference configuration, and vice versa, we use Nanson's relation, expressed as

da~{\mathbf {n}}=J~dA~{\mathbf {F}}^{{-T}}\cdot {\mathbf {N}}\,\!

where $da\,\!$ is an area of a region in the deformed configuration, $dA\,\!$ is the same area in the reference configuration, and ${\mathbf {n}}\,\!$ is the outward normal to the area element in the current configuration while ${\mathbf {N}}\,\!$ is the outward normal in the reference configuration, ${\mathbf {F}}\,\!$ is the deformation gradient, and $J=\det {\mathbf {F}}\,\!$ .

The corresponding formula for the transformation of the volume element is

dv=J~dV\,\!

Derivation of Nanson's relation (see also ^[3])

To see how this formula is derived, we start with the oriented area elements

in the reference and current configurations:

d{\mathbf {A}}=dA~{\mathbf {N}}~;~~d{\mathbf {a}}=da~{\mathbf {n}}\,\!

The reference and current volumes of an element are

dV=d{\mathbf {A}}^{{T}}\cdot d{\mathbf {L}}~;~~dv=d{\mathbf {a}}^{{T}}\cdot d{\mathbf {l}}\,\!

where $d{\mathbf {l}}={\mathbf {F}}\cdot d{\mathbf {L}}\,\!$ .

Therefore,

d{\mathbf {a}}^{{T}}\cdot d{\mathbf {l}}=dv=J~dV=J~d{\mathbf {A}}^{{T}}\cdot d{\mathbf {L}}\,\!

or,

d{\mathbf {a}}^{{T}}\cdot {\mathbf {F}}\cdot d{\mathbf {L}}=dv=J~dV=J~d{\mathbf {A}}^{{T}}\cdot d{\mathbf {L}}\,\!

so,

d{\mathbf {a}}^{{T}}\cdot {\mathbf {F}}=J~d{\mathbf {A}}^{{T}}\,\!

So we get

d{\mathbf {a}}=J~{\mathbf {F}}^{{-T}}\cdot d{\mathbf {A}}\,\!

or,

da~{\mathbf {n}}=J~dA~{\mathbf {F}}^{{-T}}\cdot {\mathbf {N}}\qquad \qquad \square \,\!

Polar decomposition of the deformation gradient tensor

Figure 3. Representation of the polar decomposition of the deformation gradient

The deformation gradient ${\mathbf {F}}\,\!$ , like any second-order tensor, can be decomposed, using the polar decomposition theorem, into a product of two second-order tensors (Truesdell and Noll, 1965): an orthogonal tensor and a positive definite symmetric tensor, i.e.

{\mathbf {F}}={\mathbf {R}}{\mathbf {U}}={\mathbf {V}}{\mathbf {R}}\,\!

where the tensor ${\mathbf {R}}\,\!$ is a proper orthogonal tensor, i.e. ${\mathbf R}^{{-1}}={\mathbf R}^{T}\,\!$ and $\det {\mathbf R}=+1\,\!$ , representing a rotation; the tensor ${\mathbf {U}}\,\!$ is the right stretch tensor; and ${\mathbf {V}}\,\!$ the left stretch tensor. The terms right and left means that they are to the right and left of the rotation tensor ${\mathbf {R}}\,\!$ , respectively. ${\mathbf {U}}\,\!$ and ${\mathbf {V}}\,\!$ are both positive definite, i.e. ${\mathbf x}\cdot {\mathbf U}\cdot {\mathbf x}\geq 0\,\!$ and ${\mathbf x}\cdot {\mathbf V}\cdot {\mathbf x}\geq 0\,\!$ , and symmetric tensors, i.e. ${\mathbf U}={\mathbf U}^{T}\,\!$ and ${\mathbf V}={\mathbf V}^{T}\,\!$ , of second order.

This decomposition implies that the deformation of a line element $d{\mathbf X}\,\!$ in the undeformed configuration onto $d{\mathbf x}\,\!$ in the deformed configuration, i.e. $d{\mathbf x}={\mathbf F}\,d{\mathbf X}\,\!$ , may be obtained either by first stretching the element by ${\mathbf U}\,\!$ , i.e. $d{\mathbf x}'={\mathbf U}\,d{\mathbf X}\,\!$ , followed by a rotation ${\mathbf R}\,\!$ , i.e. $d{\mathbf x}={\mathbf R}\,d{\mathbf x}'\,\!$ ; or equivalently, by applying a rigid rotation ${\mathbf R}\,\!$ first, i.e. $d{\mathbf x}'={\mathbf R}\,d{\mathbf X}\,\!$ , followed later by a stretching ${\mathbf V}\,\!$ , i.e. $d{\mathbf x}={\mathbf V}\,d{\mathbf x}'\,\!$ (See Figure 3).

Due to the orthogonality of $\mathbf {R}$

{\mathbf V}={\mathbf R}\cdot {\mathbf U}\cdot {\mathbf R}^{T}\,\!

so that ${\mathbf U}\,\!$ and ${\mathbf V}\,\!$ have the same eigenvalues or principal stretches, but different eigenvectors or principal directions ${\mathbf {N}}_{i}\,\!$ and ${\mathbf {n}}_{i}\,\!$ , respectively. The principal directions are related by

{\mathbf {n}}_{i}={\mathbf {R}}{\mathbf {N}}_{i}.\,\!

This polar decomposition is unique as ${\mathbf F}\,\!$ is non-symmetric.

Deformation tensors

Several rotation-independent deformation tensors are used in mechanics. In solid mechanics, the most popular of these are the right and left Cauchy–Green deformation tensors.

Since a pure rotation should not induce any stresses in a deformable body, it is often convenient to use rotation-independent measures of deformation in continuum mechanics. As a rotation followed by its inverse rotation leads to no change ( $\mathbf{R}\mathbf{R}^T=\mathbf{R}^T\mathbf{R}=\mathbf{I}\,\!$ ) we can exclude the rotation by multiplying ${\mathbf {F}}\,\!$ by its transpose.

The right Cauchy–Green deformation tensor

In 1839, George Green introduced a deformation tensor known as the right Cauchy–Green deformation tensor or Green's deformation tensor, defined as:^[4]^[5]

{\mathbf C}={\mathbf F}^{T}{\mathbf F}={\mathbf U}^{2}\qquad {\text{or}}\qquad C_{{IJ}}=F_{{kI}}~F_{{kJ}}={\frac {\partial x_{k}}{\partial X_{I}}}{\frac {\partial x_{k}}{\partial X_{J}}}.\,\!

Physically, the Cauchy–Green tensor gives us the square of local change in distances due to deformation, i.e. $d\mathbf {x} ^{2}=d\mathbf {X} \cdot \mathbf {C} \cdot d\mathbf {X} \,\!$

Invariants of ${\mathbf {C}}\,\!$ are often used in the expressions for strain energy density functions. The most commonly used invariants are

{\begin{aligned}I_{1}^{C}&:={\text{tr}}({\mathbf {C}})=C_{{II}}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}\\I_{2}^{C}&:={\tfrac {1}{2}}\left[({\text{tr}}~{\mathbf {C}})^{2}-{\text{tr}}({\mathbf {C}}^{2})\right]={\tfrac {1}{2}}\left[(C_{{JJ}})^{2}-C_{{IK}}C_{{KI}}\right]=\lambda _{1}^{2}\lambda _{2}^{2}+\lambda _{2}^{2}\lambda _{3}^{2}+\lambda _{3}^{2}\lambda _{1}^{2}\\I_{3}^{C}&:=\det({\mathbf {C}})=\lambda _{1}^{2}\lambda _{2}^{2}\lambda _{3}^{2}.\end{aligned}}\,\!

where $\lambda _{i}\,\!$ are stretch ratios for the unit fibers that are initially oriented along the directions of three axis in the coordinate systems.

The Finger deformation tensor

The IUPAC recommends^[5] that the inverse of the right Cauchy–Green deformation tensor (called the Cauchy tensor in that document), i. e., ${\mathbf C}^{{-1}}$ , be called the Finger tensor. However, that nomenclature is not universally accepted in applied mechanics.

{\mathbf {f}}={\mathbf C}^{{-1}}={\mathbf F}^{{-1}}{\mathbf F}^{{-T}}\qquad {\text{or}}\qquad f_{{IJ}}={\frac {\partial X_{I}}{\partial x_{k}}}{\frac {\partial X_{J}}{\partial x_{k}}}\,\!

The left Cauchy–Green or finger deformation tensor

Reversing the order of multiplication in the formula for the right Green–Cauchy deformation tensor leads to the left Cauchy–Green deformation tensor which is defined as:

{\mathbf B}={\mathbf F}{\mathbf F}^{T}={\mathbf V}^{2}\qquad {\text{or}}\qquad B_{{ij}}={\frac {\partial x_{i}}{\partial X_{K}}}{\frac {\partial x_{j}}{\partial X_{K}}}\,\!

The left Cauchy–Green deformation tensor is often called the Finger deformation tensor, named after Josef Finger (1894).^[5]^[6]^[7]

Invariants of ${\mathbf {B}}\,\!$ are also used in the expressions for strain energy density functions. The conventional invariants are defined as

{\begin{aligned}I_{1}&:={\text{tr}}({\mathbf {B}})=B_{{ii}}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}\\I_{2}&:={\tfrac {1}{2}}\left[({\text{tr}}~{\mathbf {B}})^{2}-{\text{tr}}({\mathbf {B}}^{2})\right]={\tfrac {1}{2}}\left(B_{{ii}}^{2}-B_{{jk}}B_{{kj}}\right)=\lambda _{1}^{2}\lambda _{2}^{2}+\lambda _{2}^{2}\lambda _{3}^{2}+\lambda _{3}^{2}\lambda _{1}^{2}\\I_{3}&:=\det {\mathbf {B}}=J^{2}=\lambda _{1}^{2}\lambda _{2}^{2}\lambda _{3}^{2}\end{aligned}}\,\!

where $J:=\det {\mathbf {F}}\,\!$ is the determinant of the deformation gradient.

For nearly incompressible materials, a slightly different set of invariants is used:

({\bar {I}}_{1}:=J^{{-2/3}}I_{1}~;~~{\bar {I}}_{2}:=J^{{-4/3}}I_{2}~;~~J=1)~.\,\!

The Cauchy deformation tensor

Earlier in 1828,^[8] Augustin Louis Cauchy introduced a deformation tensor defined as the inverse of the left Cauchy–Green deformation tensor, ${\mathbf B}^{{-1}}\,\!$ . This tensor has also been called the Piola tensor^[5] and the Finger tensor^[9] in the rheology and fluid dynamics literature.

{\mathbf {c}}={\mathbf B}^{{-1}}={\mathbf F}^{{-T}}{\mathbf F}^{{-1}}\qquad {\text{or}}\qquad c_{{ij}}={\frac {\partial X_{K}}{\partial x_{i}}}{\frac {\partial X_{K}}{\partial x_{j}}}\,\!

Spectral representation

If there are three distinct principal stretches $\lambda _{i}\,\!$ , the spectral decompositions of ${\mathbf {C}}\,\!$ and ${\mathbf {B}}\,\!$ is given by

{\mathbf {C}}=\sum _{{i=1}}^{3}\lambda _{i}^{2}{\mathbf {N}}_{i}\otimes {\mathbf {N}}_{i}\qquad {\text{and}}\qquad {\mathbf {B}}=\sum _{{i=1}}^{3}\lambda _{i}^{2}{\mathbf {n}}_{i}\otimes {\mathbf {n}}_{i}\,\!

Furthermore,

{\mathbf U}=\sum _{{i=1}}^{3}\lambda _{i}{\mathbf N}_{i}\otimes {\mathbf N}_{i}~;~~{\mathbf V}=\sum _{{i=1}}^{3}\lambda _{i}{\mathbf n}_{i}\otimes {\mathbf n}_{i}\,\!

{\mathbf R}=\sum _{{i=1}}^{3}{\mathbf n}_{i}\otimes {\mathbf N}_{i}~;~~{\mathbf F}=\sum _{{i=1}}^{3}\lambda _{i}{\mathbf n}_{i}\otimes {\mathbf N}_{i}\,\!

Observe that

{\mathbf {V}}={\mathbf {R}}~{\mathbf {U}}~{\mathbf {R}}^{T}=\sum _{{i=1}}^{3}\lambda _{i}~{\mathbf {R}}~({\mathbf {N}}_{i}\otimes {\mathbf {N}}_{i})~{\mathbf {R}}^{T}=\sum _{{i=1}}^{3}\lambda _{i}~({\mathbf {R}}~{\mathbf {N}}_{i})\otimes ({\mathbf {R}}~{\mathbf {N}}_{i})\,\!

Therefore the uniqueness of the spectral decomposition also implies that ${\mathbf {n}}_{i}={\mathbf {R}}~{\mathbf {N}}_{i}\,\!$ . The left stretch ( ${\mathbf {V}}\,\!$ ) is also called the spatial stretch tensor while the right stretch ( ${\mathbf {U}}\,\!$ ) is called the material stretch tensor.

The effect of ${\mathbf {F}}\,\!$ acting on ${\mathbf {N}}_{i}\,\!$ is to stretch the vector by $\lambda _{i}\,\!$ and to rotate it to the new orientation ${\mathbf {n}}_{i}\,\!$ , i.e.,

{\mathbf {F}}~{\mathbf {N}}_{i}=\lambda _{i}~({\mathbf {R}}~{\mathbf {N}}_{i})=\lambda _{i}~{\mathbf {n}}_{i}\,\!

In a similar vein,

{\mathbf {F}}^{{-T}}~{\mathbf {N}}_{i}={\cfrac {1}{\lambda _{i}}}~{\mathbf {n}}_{i}~;~~{\mathbf {F}}^{T}~{\mathbf {n}}_{i}=\lambda _{i}~{\mathbf {N}}_{i}~;~~{\mathbf {F}}^{{-1}}~{\mathbf {n}}_{i}={\cfrac {1}{\lambda _{i}}}~{\mathbf {N}}_{i}~.\,\!

Examples

Uniaxial extension of an incompressible material

This is the case where a specimen is stretched in 1-direction with a stretch ratio of ${\mathbf {\alpha =\alpha _{1}}}\,\!$ . If the volume remains constant, the contraction in the other two directions is such that ${\mathbf {\alpha _{1}\alpha _{2}\alpha _{3}=1}}\,\!$ or ${\mathbf {\alpha _{2}=\alpha _{3}=\alpha ^{{-0.5}}}}\,\!$ . Then:

{\mathbf {F}}={\begin{bmatrix}\alpha &0&0\\0&\alpha ^{{-0.5}}&0\\0&0&\alpha ^{{-0.5}}\end{bmatrix}}\,\!

{\mathbf {B}}={\mathbf {C}}={\begin{bmatrix}\alpha ^{2}&0&0\\0&\alpha ^{{-1}}&0\\0&0&\alpha ^{{-1}}\end{bmatrix}}\,\!

Simple shear

${\mathbf {F}}={\begin{bmatrix}1&\gamma &0\\0&1&0\\0&0&1\end{bmatrix}}\,\!$

${\mathbf {B}}={\begin{bmatrix}1+\gamma ^{2}&\gamma &0\\\gamma &1&0\\0&0&1\end{bmatrix}}\,\!$

${\mathbf {C}}={\begin{bmatrix}1&\gamma &0\\\gamma &1+\gamma ^{2}&0\\0&0&1\end{bmatrix}}\,\!$

Rigid body rotation

${\mathbf {F}}={\begin{bmatrix}\cos \theta &\sin \theta &0\\-\sin \theta &\cos \theta &0\\0&0&1\end{bmatrix}}\,\!$

${\mathbf {B}}={\mathbf {C}}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}={\mathbf {1}}\,\!$

Derivatives of stretch

Derivatives of the stretch with respect to the right Cauchy–Green deformation tensor are used to derive the stress-strain relations of many solids, particularly hyperelastic materials. These derivatives are

{\cfrac {\partial \lambda _{i}}{\partial {\mathbf {C}}}}={\cfrac {1}{2\lambda _{i}}}~{\mathbf {N}}_{i}\otimes {\mathbf {N}}_{i}={\cfrac {1}{2\lambda _{i}}}~{\mathbf {R}}^{T}~({\mathbf {n}}_{i}\otimes {\mathbf {n}}_{i})~{\mathbf {R}}~;~~i=1,2,3\,\!

and follow from the observations that

{\mathbf {C}}:({\mathbf {N}}_{i}\otimes {\mathbf {N}}_{i})=\lambda _{i}^{2}~;~~~~{\cfrac {\partial {\mathbf {C}}}{\partial {\mathbf {C}}}}={\mathsf {I}}^{{(s)}}~;~~~~{\mathsf {I}}^{{(s)}}:({\mathbf {N}}_{i}\otimes {\mathbf {N}}_{i})={\mathbf {N}}_{i}\otimes {\mathbf {N}}_{i}.\,\!

Physical interpretation of deformation tensors

Let ${\mathbf {X}}=X^{i}~{\boldsymbol {E}}_{i}$ be a Cartesian coordinate system defined on the undeformed body and let ${\mathbf {x}}=x^{i}~{\boldsymbol {E}}_{i}$ be another system defined on the deformed body. Let a curve $\mathbf {X} (s)$ in the undeformed body be parametrized using $s\in [0,1]$ . Its image in the deformed body is ${\mathbf {x}}({\mathbf {X}}(s))$ .

The undeformed length of the curve is given by

l_{X}=\int _{0}^{1}\left|{\cfrac {d{\mathbf {X}}}{ds}}\right|~ds=\int _{0}^{1}{\sqrt {{\cfrac {d{\mathbf {X}}}{ds}}\cdot {\cfrac {d{\mathbf {X}}}{ds}}}}~ds=\int _{0}^{1}{\sqrt {{\cfrac {d{\mathbf {X}}}{ds}}\cdot {\boldsymbol {I}}\cdot {\cfrac {d{\mathbf {X}}}{ds}}}}~ds

After deformation, the length becomes

{\begin{aligned}l_{x}&=\int _{0}^{1}\left|{\cfrac {d{\mathbf {x}}}{ds}}\right|~ds=\int _{0}^{1}{\sqrt {{\cfrac {d{\mathbf {x}}}{ds}}\cdot {\cfrac {d{\mathbf {x}}}{ds}}}}~ds=\int _{0}^{1}{\sqrt {\left({\cfrac {d{\mathbf {x}}}{d{\mathbf {X}}}}\cdot {\cfrac {d{\mathbf {X}}}{ds}}\right)\cdot \left({\cfrac {d{\mathbf {x}}}{d{\mathbf {X}}}}\cdot {\cfrac {d{\mathbf {X}}}{ds}}\right)}}~ds\\&=\int _{0}^{1}{\sqrt {{\cfrac {d{\mathbf {X}}}{ds}}\cdot \left[\left({\cfrac {d{\mathbf {x}}}{d{\mathbf {X}}}}\right)^{T}\cdot {\cfrac {d{\mathbf {x}}}{d{\mathbf {X}}}}\right]\cdot {\cfrac {d{\mathbf {X}}}{ds}}}}~ds\end{aligned}}

Note that the right Cauchy–Green deformation tensor is defined as

{\boldsymbol {C}}:={\boldsymbol {F}}^{T}\cdot {\boldsymbol {F}}=\left({\cfrac {d{\mathbf {x}}}{d{\mathbf {X}}}}\right)^{T}\cdot {\cfrac {d{\mathbf {x}}}{d{\mathbf {X}}}}

Hence,

l_{x}=\int _{0}^{1}{\sqrt {{\cfrac {d{\mathbf {X}}}{ds}}\cdot {\boldsymbol {C}}\cdot {\cfrac {d{\mathbf {X}}}{ds}}}}~ds

which indicates that changes in length are characterized by ${\boldsymbol {C}}$ .

Finite strain tensors

The concept of strain is used to evaluate how much a given displacement differs locally from a rigid body displacement.^[1]^[10] One of such strains for large deformations is the Lagrangian finite strain tensor, also called the Green-Lagrangian strain tensor or Green – St-Venant strain tensor, defined as

{\mathbf E}={\frac {1}{2}}({\mathbf C}-{\mathbf I})\qquad {\text{or}}\qquad E_{{KL}}={\frac {1}{2}}\left({\frac {\partial x_{j}}{\partial X_{K}}}{\frac {\partial x_{j}}{\partial X_{L}}}-\delta _{{KL}}\right)\,\!

or as a function of the displacement gradient tensor

{\mathbf E}={\frac {1}{2}}\left[(\nabla _{{{\mathbf X}}}{\mathbf u})^{T}+\nabla _{{{\mathbf X}}}{\mathbf u}+(\nabla _{{{\mathbf X}}}{\mathbf u})^{T}\cdot \nabla _{{{\mathbf X}}}{\mathbf u}\right]\,\!

E_{{KL}}={\frac {1}{2}}\left({\frac {\partial u_{K}}{\partial X_{L}}}+{\frac {\partial u_{L}}{\partial X_{K}}}+{\frac {\partial u_{M}}{\partial X_{K}}}{\frac {\partial u_{M}}{\partial X_{L}}}\right)\,\!

The Green-Lagrangian strain tensor is a measure of how much ${\mathbf C}\,\!$ differs from ${\mathbf I}\,\!$ .

The Eulerian-Almansi finite strain tensor, referenced to the deformed configuration, i.e. Eulerian description, is defined as

{\mathbf e}={\frac {1}{2}}({\mathbf I}-{\mathbf c})\qquad {\text{or}}\qquad e_{{rs}}={\frac {1}{2}}\left(\delta _{{rs}}-{\frac {\partial X_{M}}{\partial x_{r}}}{\frac {\partial X_{M}}{\partial x_{s}}}\right)\,\!

or as a function of the displacement gradients we have

e_{{ij}}={\frac {1}{2}}\left({\frac {\partial u_{i}}{\partial x_{j}}}+{\frac {\partial u_{j}}{\partial x_{i}}}-{\frac {\partial u_{k}}{\partial x_{i}}}{\frac {\partial u_{k}}{\partial x_{j}}}\right)\,\!

Derivation of the Lagrangian and Eulerian finite strain tensors

A measure of deformation is the difference between the squares of the differential line element

d{\mathbf X}\,\!

, in the undeformed configuration, and

d{\mathbf x}\,\!

, in the deformed configuration (Figure 2). Deformation has occurred if the difference is non zero, otherwise a rigid-body displacement has occurred. Thus we have,

d{\mathbf {x}}^{2}-d{\mathbf {X}}^{2}=d{\mathbf x}\cdot d{\mathbf x}-d{\mathbf X}\cdot d{\mathbf X}\qquad {\text{or}}\qquad (dx)^{2}-(dX)^{2}=dx_{j}dx_{j}-dX_{M}\,dX_{M}\,\!

In the Lagrangian description, using the material coordinates as the frame of reference, the linear transformation between the differential lines is

d{\mathbf x}={\frac {\partial {\mathbf x}}{\partial {\mathbf X}}}\,d{\mathbf X}={\mathbf F}\,d{\mathbf {X}}\qquad {\text{or}}\qquad dx_{j}={\frac {\partial x_{j}}{\partial X_{M}}}\,dX_{M}\,\!

Then we have,

{\begin{aligned}d{\mathbf {x}}^{2}&=d{\mathbf x}\cdot d{\mathbf x}\\&={\mathbf F}\cdot d{\mathbf X}\cdot {\mathbf F}\cdot d{\mathbf X}\\&=d{\mathbf X}\cdot {\mathbf F}^{T}{\mathbf F}\cdot d{\mathbf X}\\&=d{\mathbf X}\cdot {\mathbf C}\cdot d{\mathbf X}\end{aligned}}\qquad {\text{or}}\qquad {\begin{aligned}(dx)^{2}&=dx_{j}\,dx_{j}\\&={\frac {\partial x_{j}}{\partial X_{K}}}{\frac {\partial x_{j}}{\partial X_{L}}}\,dX_{K}\,dX_{L}\\&=C_{{KL}}\,dX_{K}\,dX_{L}\\\end{aligned}}\,\!

where $C_{{KL}}\,\!$ are the components of the right Cauchy–Green deformation tensor, ${\mathbf C}={\mathbf F}^{T}{\mathbf F}\,\!$ . Then, replacing this equation into the first equation we have,

{\begin{aligned}d{\mathbf {x}}^{2}-d{\mathbf {X}}^{2}&=d{\mathbf X}\cdot {\mathbf C}\cdot d{\mathbf X}-d{\mathbf X}\cdot d{\mathbf X}\\&=d{\mathbf X}\cdot ({\mathbf C}-{\mathbf I})\cdot d{\mathbf X}\\&=d{\mathbf X}\cdot 2{\mathbf E}\cdot d{\mathbf X}\\\end{aligned}}\,\!

{\begin{aligned}(dx)^{2}-(dX)^{2}&={\frac {\partial x_{j}}{\partial X_{K}}}{\frac {\partial x_{j}}{\partial X_{L}}}\,dX_{K}\,dX_{L}-dX_{M}\,dX_{M}\\&=\left({\frac {\partial x_{j}}{\partial X_{K}}}{\frac {\partial x_{j}}{\partial X_{L}}}-\delta _{{KL}}\right)\,dX_{K}\,dX_{L}\\&=2E_{{KL}}\,dX_{K}\,dX_{L}\end{aligned}}\,\!

where $E_{{KL}}\,\!$ , are the components of a second-order tensor called the Green – St-Venant strain tensor or the Lagrangian finite strain tensor,

{\mathbf E}={\frac {1}{2}}({\mathbf C}-{\mathbf I})\qquad {\text{or}}\qquad E_{{KL}}={\frac {1}{2}}\left({\frac {\partial x_{j}}{\partial X_{K}}}{\frac {\partial x_{j}}{\partial X_{L}}}-\delta _{{KL}}\right)\,\!

In the Eulerian description, using the spatial coordinates as the frame of reference, the linear transformation between the differential lines is

d{\mathbf {X}}={\frac {\partial {\mathbf {X}}}{\partial {\mathbf {x}}}}d{\mathbf {x}}={\mathbf F}^{{-1}}\,d{\mathbf {x}}={\mathbf {H}}\,d{\mathbf {x}}\qquad {\text{or}}\qquad dX_{M}={\frac {\partial X_{M}}{\partial x_{n}}}\,dx_{n}\,\!

where ${\frac {\partial X_{M}}{\partial x_{n}}}\,\!$ are the components of the spatial deformation gradient tensor, ${\mathbf {H}}\,\!$ . Thus we have

{\begin{aligned}d{\mathbf {X}}^{2}&=d{\mathbf X}\cdot d{\mathbf X}\\&={\mathbf F}^{{-1}}\cdot d{\mathbf x}\cdot {\mathbf F}^{{-1}}\cdot d{\mathbf x}\\&=d{\mathbf x}\cdot {\mathbf F}^{{-T}}{\mathbf F}^{{-1}}\cdot d{\mathbf x}\\&=d{\mathbf x}\cdot {\mathbf c}\cdot d{\mathbf x}\end{aligned}}\qquad {\text{or}}\qquad {\begin{aligned}(dX)^{2}&=dX_{M}\,dX_{M}\\&={\frac {\partial X_{M}}{\partial x_{r}}}{\frac {\partial X_{M}}{\partial x_{s}}}\,dx_{r}\,dx_{s}\\&=c_{{rs}}\,dx_{r}\,dx_{s}\\\end{aligned}}\,\!

where the second order tensor $c_{{rs}}\,\!$ is called Cauchy's deformation tensor, ${\mathbf c}={\mathbf F}^{{-T}}{\mathbf F}^{{-1}}\,\!$ . Then we have,

{\begin{aligned}d{\mathbf {x}}^{2}-d{\mathbf {X}}^{2}&=d{\mathbf x}\cdot d{\mathbf x}-d{\mathbf x}\cdot {\mathbf c}\cdot d{\mathbf x}\\&=d{\mathbf x}\cdot ({\mathbf I}-{\mathbf c})\cdot d{\mathbf x}\\&=d{\mathbf x}\cdot 2{\mathbf e}\cdot d{\mathbf x}\\\end{aligned}}\,\!

{\begin{aligned}(dx)^{2}-(dX)^{2}&=dx_{j}\,dx_{j}-{\frac {\partial X_{M}}{\partial x_{r}}}{\frac {\partial X_{M}}{\partial x_{s}}}\,dx_{r}\,dx_{s}\\&=\left(\delta _{{rs}}-{\frac {\partial X_{M}}{\partial x_{r}}}{\frac {\partial X_{M}}{\partial x_{s}}}\right)\,dx_{r}\,dx_{s}\\&=2e_{{rs}}\,dx_{r}\,dx_{s}\end{aligned}}\,\!

where $e_{{rs}}\,\!$ , are the components of a second-order tensor called the Eulerian-Almansi finite strain tensor,

{\mathbf e}={\frac {1}{2}}({\mathbf I}-{\mathbf c})\qquad {\text{or}}\qquad e_{{rs}}={\frac {1}{2}}\left(\delta _{{rs}}-{\frac {\partial X_{M}}{\partial x_{r}}}{\frac {\partial X_{M}}{\partial x_{s}}}\right)\,\!

Both the Lagrangian and Eulerian finite strain tensors can be conveniently expressed in terms of the displacement gradient tensor. For the Lagrangian strain tensor, first we differentiate the displacement vector ${\mathbf u}({\mathbf X},t)\,\!$ with respect to the material coordinates $X_{M}\,\!$ to obtain the material displacement gradient tensor, $\nabla _{{{\mathbf X}}}{\mathbf u}\,\!$

{\begin{aligned}{\mathbf u}({\mathbf X},t)&={\mathbf x}({\mathbf X},t)-{\mathbf X}\\\nabla _{{{\mathbf X}}}{\mathbf u}&={\mathbf F}-{\mathbf I}\\{\mathbf F}&=\nabla _{{{\mathbf X}}}{\mathbf u}+{\mathbf I}\\\end{aligned}}\qquad {\text{or}}\qquad {\begin{aligned}u_{i}&=x_{i}-\delta _{{iJ}}X_{J}\\\delta _{{iJ}}U_{J}&=x_{i}-\delta _{{iJ}}X_{J}\\x_{i}&=\delta _{{iJ}}\left(U_{J}+X_{J}\right)\\{\frac {\partial x_{i}}{\partial X_{K}}}&=\delta _{{iJ}}\left({\frac {\partial U_{J}}{\partial X_{K}}}+\delta _{{JK}}\right)\\\end{aligned}}\,\!

Replacing this equation into the expression for the Lagrangian finite strain tensor we have

{\begin{aligned}{\mathbf E}&={\frac {1}{2}}\left({\mathbf F}^{T}{\mathbf F}-{\mathbf I}\right)\\&={\frac {1}{2}}\left[\left\{(\nabla _{{{\mathbf X}}}{\mathbf u})^{T}+{\mathbf I}\right\}\left(\nabla _{{{\mathbf X}}}{\mathbf u}+{\mathbf I}\right)-{\mathbf I}\right]\\&={\frac {1}{2}}\left[(\nabla _{{{\mathbf X}}}{\mathbf u})^{T}+\nabla _{{{\mathbf X}}}{\mathbf u}+(\nabla _{{{\mathbf X}}}{\mathbf u})^{T}\cdot \nabla _{{{\mathbf X}}}{\mathbf u}\right]\\\end{aligned}}\,\!

{\begin{aligned}E_{{KL}}&={\frac {1}{2}}\left({\frac {\partial x_{j}}{\partial X_{K}}}{\frac {\partial x_{j}}{\partial X_{L}}}-\delta _{{KL}}\right)\\&={\frac {1}{2}}\left[\delta _{{jM}}\left({\frac {\partial U_{M}}{\partial X_{K}}}+\delta _{{MK}}\right)\delta _{{jN}}\left({\frac {\partial U_{N}}{\partial X_{L}}}+\delta _{{NL}}\right)-\delta _{{KL}}\right]\\&={\frac {1}{2}}\left[\delta _{{MN}}\left({\frac {\partial U_{M}}{\partial X_{K}}}+\delta _{{MK}}\right)\left({\frac {\partial U_{N}}{\partial X_{L}}}+\delta _{{NL}}\right)-\delta _{{KL}}\right]\\&={\frac {1}{2}}\left[\left({\frac {\partial U_{M}}{\partial X_{K}}}+\delta _{{MK}}\right)\left({\frac {\partial U_{M}}{\partial X_{L}}}+\delta _{{ML}}\right)-\delta _{{KL}}\right]\\&={\frac {1}{2}}\left({\frac {\partial U_{K}}{\partial X_{L}}}+{\frac {\partial U_{L}}{\partial X_{K}}}+{\frac {\partial U_{M}}{\partial X_{K}}}{\frac {\partial U_{M}}{\partial X_{L}}}\right)\end{aligned}}\,\!

Similarly, the Eulerian-Almansi finite strain tensor can be expressed as

e_{{ij}}={\frac {1}{2}}\left({\frac {\partial u_{i}}{\partial x_{j}}}+{\frac {\partial u_{j}}{\partial x_{i}}}-{\frac {\partial u_{k}}{\partial x_{i}}}{\frac {\partial u_{k}}{\partial x_{j}}}\right)\,\!

Seth–Hill family of generalized strain tensors

B. R. Seth from the Indian Institute of Technology, Kharagpur was the first to show that the Green and Almansi strain tensors are special cases of a more general strain measure.^[11]^[12] The idea was further expanded upon by Rodney Hill in 1968.^[13] The Seth–Hill family of strain measures (also called Doyle-Ericksen tensors)^[14] can be expressed as

{\mathbf E}_{{(m)}}={\frac {1}{2m}}({\mathbf U}^{{2m}}-{\mathbf I})={\frac {1}{2m}}\left[{\mathbf {C}}^{{m}}-{\mathbf {I}}\right]\,\!

For different values of $m\,\!$ we have:

{\begin{aligned}{\mathbf E}_{{(1)}}&={\frac {1}{2}}({\mathbf U}^{{2}}-{\mathbf I})={\frac {1}{2}}({\mathbf {C}}-{\mathbf {I}})&\qquad {\text{Green-Lagrangian strain tensor}}\\{\mathbf E}_{{(1/2)}}&=({\mathbf U}-{\mathbf I})={\mathbf {C}}^{{1/2}}-{\mathbf {I}}&\qquad {\text{Biot strain tensor}}\\{\mathbf E}_{{(0)}}&=\ln {\mathbf U}={\frac {1}{2}}\,\ln {\mathbf {C}}&\qquad {\text{Logarithmic strain, Natural strain, True strain, or Hencky strain}}\\{\mathbf {E}}_{{(-1)}}&={\frac {1}{2}}\left[{\mathbf {I}}-{\mathbf {U}}^{{-2}}\right]&\qquad {\text{Almansi strain}}\end{aligned}}\,\!

The second-order approximation of these tensors is

{\mathbf {E}}_{{(m)}}={\boldsymbol {\varepsilon }}+{{\tfrac 12}}(\nabla {\mathbf {u}})^{T}\cdot \nabla {\mathbf {u}}-(1-m){\boldsymbol {\varepsilon }}^{T}\cdot {\boldsymbol {\varepsilon }}

where $\boldsymbol{\varepsilon}$ is the infinitesimal strain tensor.

Many other different definitions of tensors $\mathbf {E}$ are admissible, provided that they all satisfy the conditions that:^[15]

$\mathbf {E}$ vanishes for all rigid-body motions
the dependence of $\mathbf {E}$ on the displacement gradient tensor $\nabla \mathbf {u}$ is continuous, continuously differentiable and monotonic
it is also desired that $\mathbf {E}$ reduces to the infinitesimal strain tensor $\boldsymbol{\varepsilon}$ as the norm $|\nabla {\mathbf {u}}|\to 0$

An example is the set of tensors

{\mathbf {E}}^{{(n)}}=\left({{\mathbf U}}^{n}-{{\mathbf U}}^{{-n}}\right)/2n

which do not belong to the Seth–Hill class, but have the same 2nd-order approximation as the Seth–Hill measures at $m=0$ for any value of $n$ .^[16]

Stretch ratio

The stretch ratio is a measure of the extensional or normal strain of a differential line element, which can be defined at either the undeformed configuration or the deformed configuration.

The stretch ratio for the differential element $d{\mathbf X}=dX{\mathbf N}\,\!$ (Figure) in the direction of the unit vector ${\mathbf N}\,\!$ at the material point $P\,\!$ , in the undeformed configuration, is defined as

\Lambda _{{({\mathbf N})}}={\frac {dx}{dX}}\,\!

where $dx\,\!$ is the deformed magnitude of the differential element $d{\mathbf X}\,\!$ .

Similarly, the stretch ratio for the differential element $d{\mathbf x}=dx{\mathbf n}\,\!$ (Figure), in the direction of the unit vector ${\mathbf n}\,\!$ at the material point $p\,\!$ , in the deformed configuration, is defined as

{\frac {1}{\Lambda _{{({\mathbf n})}}}}={\frac {dX}{dx}}.\,\!

The normal strain $e_{{{\mathbf N}}}\,\!$ in any direction ${\mathbf N}\,\!$ can be expressed as a function of the stretch ratio,

e_{{({\mathbf N})}}={\frac {dx-dX}{dX}}=\Lambda _{{({\mathbf N})}}-1.\,\!

This equation implies that the normal strain is zero, i.e. no deformation, when the stretch is equal to unity. Some materials, such as elastometers can sustain stretch ratios of 3 or 4 before they fail, whereas traditional engineering materials, such as concrete or steel, fail at much lower stretch ratios, perhaps of the order of 1.001 (reference?)

Physical interpretation of the finite strain tensor

The diagonal components $E_{{KL}}\,\!$ of the Lagrangian finite strain tensor are related to the normal strain, e.g.

E_{{11}}=e_{{({\mathbf I}_{1})}}+{\frac {1}{2}}e_{{({\mathbf I}_{1})}}^{2}\,\!

where $e_{{({\mathbf I}_{1})}}\,\!$ is the normal strain or engineering strain in the direction ${\mathbf I}_{1}\,\!$ .

The off-diagonal components $E_{{KL}}\,\!$ of the Lagrangian finite strain tensor are related to shear strain, e.g.

E_{{12}}={\frac {1}{2}}{\sqrt {2E_{{11}}+1}}{\sqrt {2E_{{22}}+1}}\sin \phi _{{12}}\,\!

where $\phi _{{12}}\,\!$ is the change in the angle between two line elements that were originally perpendicular with directions ${\mathbf I}_{1}\,\!$ and ${\mathbf I}_{2}\,\!$ , respectively.

Under certain circumstances, i.e. small displacements and small displacement rates, the components of the Lagrangian finite strain tensor may be approximated by the components of the infinitesimal strain tensor

Derivation of the physical interpretation of the Lagrangian and Eulerian finite strain tensors

The stretch ratio for the differential element

d{\mathbf X}=dX{\mathbf N}\,\!

(Figure) in the direction of the unit vector

{\mathbf N}\,\!

at the material point

P\,\!

, in the undeformed configuration, is defined as

\Lambda _{{({\mathbf N})}}={\frac {dx}{dX}}\,\!

where $dx\,\!$ is the deformed magnitude of the differential element $d{\mathbf X}\,\!$ .

{\frac {1}{\Lambda _{{({\mathbf n})}}}}={\frac {dX}{dx}}\,\!

The square of the stretch ratio is defined as

\Lambda _{{({\mathbf N})}}^{2}=\left({\frac {dx}{dX}}\right)^{2}\,\!

Knowing that

(dx)^{2}=C_{{KL}}dX_{K}dX_{L}\,\!

we have

\Lambda _{{({\mathbf N})}}^{2}=C_{{KL}}N_{K}N_{L}\,\!

where $N_{K}\,\!$ and $N_{L}\,\!$ are unit vectors.

The normal strain or engineering strain $e_{{{\mathbf N}}}\,\!$ in any direction ${\mathbf N}\,\!$ can be expressed as a function of the stretch ratio,

e_{{({\mathbf N})}}={\frac {dx-dX}{dX}}=\Lambda _{{({\mathbf N})}}-1\,\!

Thus, the normal strain in the direction ${\mathbf I}_{1}\,\!$ at the material point $P\,\!$ may be expressed in terms of the stretch ratio as

{\begin{aligned}e_{{({\mathbf I}_{1})}}={\frac {dx_{1}-dX_{1}}{dX_{1}}}&=\Lambda _{{({\mathbf I}_{1})}}-1\\&={\sqrt {C_{{11}}}}-1={\sqrt {\delta _{{11}}+2E_{{11}}}}-1\\&={\sqrt {1+2E_{{11}}}}-1\end{aligned}}\,\!

solving for $E_{{11}}\,\!$ we have

${\begin{aligned}2E_{{11}}&={\frac {(dx_{1})^{2}-(dX_{1})^{2}}{(dX_{1})^{2}}}\\E_{{11}}&=\left({\frac {dx_{1}-dX_{1}}{dX_{1}}}\right)+{\frac {1}{2}}\left({\frac {dx_{1}-dX_{1}}{dX_{1}}}\right)^{2}\\&=e_{{({\mathbf I}_{1})}}+{\frac {1}{2}}e_{{({\mathbf I}_{1})}}^{2}\end{aligned}}\,\!$

The shear strain, or change in angle between two line elements $d{\mathbf X}_{1}\,\!$ and $d{\mathbf X}_{2}\,\!$ initially perpendicular, and oriented in the principal directions ${\mathbf I}_{1}\,\!$ and ${\mathbf I}_{2}\,\!$ , respectivelly, can also be expressed as a function of the stretch ratio. From the dot product between the deformed lines $d{\mathbf x}_{1}\,\!$ and $d{\mathbf x}_{2}\,\!$ we have

{\begin{aligned}d{\mathbf x}_{1}\cdot d{\mathbf x}_{2}&=dx_{1}dx_{2}\cos \theta _{{12}}\\{\mathbf F}\cdot d{\mathbf X}_{1}\cdot {\mathbf F}\cdot d{\mathbf X}_{2}&={\sqrt {d{\mathbf X}_{1}\cdot {\mathbf F}^{T}\cdot {\mathbf F}\cdot d{\mathbf X}_{1}}}\cdot {\sqrt {d{\mathbf X}_{2}\cdot {\mathbf F}^{T}\cdot {\mathbf F}\cdot d{\mathbf X}_{2}}}\cos \theta _{{12}}\\{\frac {d{\mathbf X}_{1}\cdot {\mathbf F}^{T}\cdot {\mathbf F}\cdot d{\mathbf X}_{2}}{dX_{1}dX_{2}}}&={\frac {{\sqrt {d{\mathbf X}_{1}\cdot {\mathbf F}^{T}\cdot {\mathbf F}\cdot d{\mathbf X}_{1}}}\cdot {\sqrt {d{\mathbf X}_{2}\cdot {\mathbf F}^{T}\cdot {\mathbf F}\cdot d{\mathbf X}_{2}}}}{dX_{1}dX_{2}}}\cos \theta _{{12}}\\{\mathbf I}_{1}\cdot {\mathbf C}\cdot {\mathbf I}_{2}&=\Lambda _{{{\mathbf I}_{1}}}\Lambda _{{{\mathbf I}_{2}}}\cos \theta _{{12}}\\\end{aligned}}\,\!

where $\theta _{{12}}\,\!$ is the angle between the lines $d{\mathbf x}_{1}\,\!$ and $d{\mathbf x}_{2}\,\!$ in the deformed configuration. Defining $\phi _{{12}}\,\!$ as the shear strain or reduction in the angle between two line elements that were originally perpendicular, we have

\phi _{{12}}={\frac {\pi }{2}}-\theta _{{12}}\,\!

thus,

\cos \theta _{{12}}=\sin \phi _{{12}}\,\!

then

{\mathbf I}_{1}\cdot {\mathbf C}\cdot {\mathbf I}_{2}=\Lambda _{{{\mathbf I}_{1}}}\Lambda _{{{\mathbf I}_{2}}}\sin \phi _{{12}}\,\!

{\begin{aligned}C_{{12}}&={\sqrt {C_{{11}}}}{\sqrt {C_{{22}}}}\sin \phi _{{12}}\\2E_{{12}}+\delta _{{12}}&={\sqrt {2E_{{11}}+1}}{\sqrt {2E_{{22}}+1}}\sin \phi _{{12}}\\E_{{12}}&={\frac {1}{2}}{\sqrt {2E_{{11}}+1}}{\sqrt {2E_{{22}}+1}}\sin \phi _{{12}}\end{aligned}}\,\!

Deformation tensors in curvilinear coordinates

A representation of deformation tensors in curvilinear coordinates is useful for many problems in continuum mechanics such as nonlinear shell theories and large plastic deformations. Let ${\mathbf {x}}={\mathbf {x}}(\xi ^{1},\xi ^{2},\xi ^{3})$ be a given deformation where the space is characterized by the coordinates $(\xi ^{1},\xi ^{2},\xi ^{3})$ . The tangent vector to the coordinate curve $\xi ^{i}$ at $\mathbf {x}$ is given by

{\mathbf {g}}_{i}={\frac {\partial {\mathbf {x}}}{\partial \xi ^{i}}}

The three tangent vectors at $\mathbf {x}$ form a basis. These vectors are related the reciprocal basis vectors by

{\mathbf {g}}_{i}\cdot {\mathbf {g}}^{j}=\delta _{i}^{j}

Let us define a second-order tensor field $\boldsymbol{g}$ (also called the metric tensor) with components

g_{{ij}}:={\frac {\partial {\mathbf {x}}}{\partial \xi ^{i}}}\cdot {\frac {\partial {\mathbf {x}}}{\partial \xi ^{j}}}={\mathbf {g}}_{i}\cdot {\mathbf {g}}_{j}

The Christoffel symbols of the first kind can be expressed as

\Gamma _{{ijk}}={\tfrac {1}{2}}[({\mathbf {g}}_{i}\cdot {\mathbf {g}}_{k})_{{,j}}+({\mathbf {g}}_{j}\cdot {\mathbf {g}}_{k})_{{,i}}-({\mathbf {g}}_{i}\cdot {\mathbf {g}}_{j})_{{,k}}]

To see how the Christoffel symbols are related to the Right Cauchy–Green deformation tensor let us define two sets of bases

{\mathbf {G}}_{i}:={\frac {\partial {\mathbf {X}}}{\partial \xi ^{i}}}~;~~{\mathbf {G}}_{i}\cdot {\mathbf {G}}^{j}=\delta _{i}^{j}~;~~{\mathbf {g}}_{i}:={\frac {\partial {\mathbf {x}}}{\partial \xi ^{i}}}~;~~{\mathbf {g}}_{i}\cdot {\mathbf {g}}^{j}=\delta _{i}^{j}

The deformation gradient in curvilinear coordinates

Using the definition of the gradient of a vector field in curvilinear coordinates, the deformation gradient can be written as

{\boldsymbol {F}}={\boldsymbol {\nabla }}_{{{\mathbf {X}}}}{\mathbf {x}}={\frac {\partial {\mathbf {x}}}{\partial \xi ^{i}}}\otimes {\mathbf {G}}^{i}={\mathbf {g}}_{i}\otimes {\mathbf {G}}^{i}

The right Cauchy–Green tensor in curvilinear coordinates

The right Cauchy–Green deformation tensor is given by

{\boldsymbol {C}}={\boldsymbol {F}}^{T}\cdot {\boldsymbol {F}}=({\mathbf {G}}^{i}\otimes {\mathbf {g}}_{i})\cdot ({\mathbf {g}}_{j}\otimes {\mathbf {G}}^{j})=({\mathbf {g}}_{i}\cdot {\mathbf {g}}_{j})({\mathbf {G}}^{i}\otimes {\mathbf {G}}^{j})

If we express ${\boldsymbol {C}}$ in terms of components with respect to the basis { ${\mathbf {G}}^{i}$ } we have

{\boldsymbol {C}}=C_{{ij}}~{\mathbf {G}}^{i}\otimes {\mathbf {G}}^{j}

Therefore

C_{{ij}}={\mathbf {g}}_{i}\cdot {\mathbf {g}}_{j}=g_{{ij}}

and the Christoffel symbol of the first kind may be written in the following form.

\Gamma _{{ijk}}={\tfrac {1}{2}}[C_{{ik,j}}+C_{{jk,i}}-C_{{ij,k}}]={\tfrac {1}{2}}[({\mathbf {G}}_{i}\cdot {\boldsymbol {C}}\cdot {\mathbf {G}}_{k})_{{,j}}+({\mathbf {G}}_{j}\cdot {\boldsymbol {C}}\cdot {\mathbf {G}}_{k})_{{,i}}-({\mathbf {G}}_{i}\cdot {\boldsymbol {C}}\cdot {\mathbf {G}}_{j})_{{,k}}]

Some relations between deformation measures and Christoffel symbols

Let us consider a one-to-one mapping from ${\mathbf {X}}=\{X^{1},X^{2},X^{3}\}$ to ${\mathbf {x}}=\{x^{1},x^{2},x^{3}\}$ and let us assume that there exist two positive definite, symmetric second-order tensor fields $\boldsymbol{G}$ and $\boldsymbol{g}$ that satisfy

G_{{ij}}={\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}~g_{{\alpha \beta }}

Then,

{\frac {\partial G_{{ij}}}{\partial x^{k}}}=\left({\frac {\partial ^{2}X^{\alpha }}{\partial x^{i}\partial x^{k}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}+{\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial ^{2}X^{\beta }}{\partial x^{j}\partial x^{k}}}\right)~g_{{\alpha \beta }}+{\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}~{\frac {\partial g_{{\alpha \beta }}}{\partial x^{k}}}

Noting that

{\frac {\partial g_{{\alpha \beta }}}{\partial x^{k}}}={\frac {\partial X^{\gamma }}{\partial x^{k}}}~{\frac {\partial g_{{\alpha \beta }}}{\partial X^{\gamma }}}

and $g_{{\alpha \beta }}=g_{{\beta \alpha }}$ we have

{\begin{aligned}{\frac {\partial G_{{ij}}}{\partial x^{k}}}&=\left({\frac {\partial ^{2}X^{\alpha }}{\partial x^{i}\partial x^{k}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}+{\frac {\partial ^{2}X^{\alpha }}{\partial x^{j}\partial x^{k}}}~{\frac {\partial X^{\beta }}{\partial x^{i}}}\right)~g_{{\alpha \beta }}+{\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}~{\frac {\partial X^{\gamma }}{\partial x^{k}}}~{\frac {\partial g_{{\alpha \beta }}}{\partial X^{\gamma }}}\\{\frac {\partial G_{{ik}}}{\partial x^{j}}}&=\left({\frac {\partial ^{2}X^{\alpha }}{\partial x^{i}\partial x^{j}}}~{\frac {\partial X^{\beta }}{\partial x^{k}}}+{\frac {\partial ^{2}X^{\alpha }}{\partial x^{j}\partial x^{k}}}~{\frac {\partial X^{\beta }}{\partial x^{i}}}\right)~g_{{\alpha \beta }}+{\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{k}}}~{\frac {\partial X^{\gamma }}{\partial x^{j}}}~{\frac {\partial g_{{\alpha \beta }}}{\partial X^{\gamma }}}\\{\frac {\partial G_{{jk}}}{\partial x^{i}}}&=\left({\frac {\partial ^{2}X^{\alpha }}{\partial x^{i}\partial x^{j}}}~{\frac {\partial X^{\beta }}{\partial x^{k}}}+{\frac {\partial ^{2}X^{\alpha }}{\partial x^{i}\partial x^{k}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}\right)~g_{{\alpha \beta }}+{\frac {\partial X^{\alpha }}{\partial x^{j}}}~{\frac {\partial X^{\beta }}{\partial x^{k}}}~{\frac {\partial X^{\gamma }}{\partial x^{i}}}~{\frac {\partial g_{{\alpha \beta }}}{\partial X^{\gamma }}}\end{aligned}}

Define

{\begin{aligned}_{{(x)}}\Gamma _{{ijk}}&:={\frac {1}{2}}\left({\frac {\partial G_{{ik}}}{\partial x^{j}}}+{\frac {\partial G_{{jk}}}{\partial x^{i}}}-{\frac {\partial G_{{ij}}}{\partial x^{k}}}\right)\\_{{(X)}}\Gamma _{{\alpha \beta \gamma }}&:={\frac {1}{2}}\left({\frac {\partial g_{{\alpha \gamma }}}{\partial X^{\beta }}}+{\frac {\partial g_{{\beta \gamma }}}{\partial X^{\alpha }}}-{\frac {\partial g_{{\alpha \beta }}}{\partial X^{\gamma }}}\right)\\\end{aligned}}

Hence

_{{(x)}}\Gamma _{{ijk}}={\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}~{\frac {\partial X^{\gamma }}{\partial x^{k}}}\,_{{(X)}}\Gamma _{{\alpha \beta \gamma }}+{\frac {\partial ^{2}X^{\alpha }}{\partial x^{i}\partial x^{j}}}~{\frac {\partial X^{\beta }}{\partial x^{k}}}~g_{{\alpha \beta }}

Define

[G^{{ij}}]=[G_{{ij}}]^{{-1}}~;~~[g^{{\alpha \beta }}]=[g_{{\alpha \beta }}]^{{-1}}

Then

G^{{ij}}={\frac {\partial x^{i}}{\partial X^{\alpha }}}~{\frac {\partial x^{j}}{\partial X^{\beta }}}~g^{{\alpha \beta }}

Define the Christoffel symbols of the second kind as

_{{(x)}}\Gamma _{{ij}}^{m}:=G^{{mk}}\,_{{(x)}}\Gamma _{{ijk}}~;~~_{{(X)}}\Gamma _{{\alpha \beta }}^{\nu }:=g^{{\nu \gamma }}\,_{{(X)}}\Gamma _{{\alpha \beta \gamma }}

Then

{\begin{aligned}_{{(x)}}\Gamma _{{ij}}^{m}&=G^{{mk}}~{\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}~{\frac {\partial X^{\gamma }}{\partial x^{k}}}\,_{{(X)}}\Gamma _{{\alpha \beta \gamma }}+G^{{mk}}~{\frac {\partial ^{2}X^{\alpha }}{\partial x^{i}\partial x^{j}}}~{\frac {\partial X^{\beta }}{\partial x^{k}}}~g_{{\alpha \beta }}\\&={\frac {\partial x^{m}}{\partial X^{\nu }}}~{\frac {\partial x^{k}}{\partial X^{\rho }}}~g^{{\nu \rho }}~{\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}~{\frac {\partial X^{\gamma }}{\partial x^{k}}}\,_{{(X)}}\Gamma _{{\alpha \beta \gamma }}+{\frac {\partial x^{m}}{\partial X^{\nu }}}~{\frac {\partial x^{k}}{\partial X^{\rho }}}~g^{{\nu \rho }}~{\frac {\partial ^{2}X^{\alpha }}{\partial x^{i}\partial x^{j}}}~{\frac {\partial X^{\beta }}{\partial x^{k}}}~g_{{\alpha \beta }}\\&={\frac {\partial x^{m}}{\partial X^{\nu }}}~\delta _{\rho }^{\gamma }~g^{{\nu \rho }}~{\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}\,_{{(X)}}\Gamma _{{\alpha \beta \gamma }}+{\frac {\partial x^{m}}{\partial X^{\nu }}}~\delta _{\rho }^{\beta }~g^{{\nu \rho }}~{\frac {\partial ^{2}X^{\alpha }}{\partial x^{i}\partial x^{j}}}~g_{{\alpha \beta }}\\&={\frac {\partial x^{m}}{\partial X^{\nu }}}~g^{{\nu \gamma }}~{\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}\,_{{(X)}}\Gamma _{{\alpha \beta \gamma }}+{\frac {\partial x^{m}}{\partial X^{\nu }}}~g^{{\nu \beta }}~{\frac {\partial ^{2}X^{\alpha }}{\partial x^{i}\partial x^{j}}}~g_{{\alpha \beta }}\\&={\frac {\partial x^{m}}{\partial X^{\nu }}}~{\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\nu }+{\frac {\partial x^{m}}{\partial X^{\nu }}}~\delta _{{\alpha }}^{{\nu }}~{\frac {\partial ^{2}X^{\alpha }}{\partial x^{i}\partial x^{j}}}\end{aligned}}

Therefore

_{{(x)}}\Gamma _{{ij}}^{m}={\frac {\partial x^{m}}{\partial X^{\nu }}}~{\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\nu }+{\frac {\partial x^{m}}{\partial X^{\alpha }}}~{\frac {\partial ^{2}X^{\alpha }}{\partial x^{i}\partial x^{j}}}

The invertibility of the mapping implies that

{\begin{aligned}{\frac {\partial X^{\mu }}{\partial x^{m}}}\,_{{(x)}}\Gamma _{{ij}}^{m}&={\frac {\partial X^{\mu }}{\partial x^{m}}}~{\frac {\partial x^{m}}{\partial X^{\nu }}}~{\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\nu }+{\frac {\partial X^{\mu }}{\partial x^{m}}}~{\frac {\partial x^{m}}{\partial X^{\alpha }}}~{\frac {\partial ^{2}X^{\alpha }}{\partial x^{i}\partial x^{j}}}\\&=\delta _{\nu }^{\mu }~{\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\nu }+\delta _{\alpha }^{\mu }~{\frac {\partial ^{2}X^{\alpha }}{\partial x^{i}\partial x^{j}}}\\&={\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }+{\frac {\partial ^{2}X^{\mu }}{\partial x^{i}\partial x^{j}}}\end{aligned}}

We can also formulate a similar result in terms of derivatives with respect to $x$ . Therefore

{\begin{aligned}{\frac {\partial ^{2}X^{\mu }}{\partial x^{i}\partial x^{j}}}&={\frac {\partial X^{\mu }}{\partial x^{m}}}\,_{{(x)}}\Gamma _{{ij}}^{m}-{\frac {\partial X^{\alpha }}{\partial x^{i}}}~{\frac {\partial X^{\beta }}{\partial x^{j}}}\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }\\{\frac {\partial ^{2}x^{m}}{\partial X^{\alpha }\partial X^{\beta }}}&={\frac {\partial x^{m}}{\partial X^{\mu }}}\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }-{\frac {\partial x^{i}}{\partial X^{\alpha }}}~{\frac {\partial x^{j}}{\partial X^{\beta }}}\,_{{(x)}}\Gamma _{{ij}}^{m}\end{aligned}}

Compatibility conditions

Main article: Compatibility (mechanics)

The problem of compatibility in continuum mechanics involves the determination of allowable single-valued continuous fields on bodies. These allowable conditions leave the body without unphysical gaps or overlaps after a deformation. Most such conditions apply to simply-connected bodies. Additional conditions are required for the internal boundaries of multiply connected bodies.

Compatibility of the deformation gradient

The necessary and sufficient conditions for the existence of a compatible ${\boldsymbol {F}}$ field over a simply connected body are

{\boldsymbol {\nabla }}\times {\boldsymbol {F}}={\boldsymbol {0}}

Compatibility of the right Cauchy–Green deformation tensor

The necessary and sufficient conditions for the existence of a compatible ${\boldsymbol {C}}$ field over a simply connected body are

R_{{\alpha \beta \rho }}^{\gamma }:={\frac {\partial }{\partial X^{\rho }}}[\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\gamma }]-{\frac {\partial }{\partial X^{\beta }}}[\,_{{(X)}}\Gamma _{{\alpha \rho }}^{\gamma }]+\,_{{(X)}}\Gamma _{{\mu \rho }}^{\gamma }\,_{{(X)}}\Gamma _{{\alpha \beta }}^{\mu }-\,_{{(X)}}\Gamma _{{\mu \beta }}^{\gamma }\,_{{(X)}}\Gamma _{{\alpha \rho }}^{\mu }=0

We can show these are the mixed components of the Riemann–Christoffel curvature tensor. Therefore the necessary conditions for ${\boldsymbol {C}}$ -compatibility are that the Riemann–Christoffel curvature of the deformation is zero.

Compatibility of the left Cauchy–Green deformation tensor

No general sufficiency conditions are known for the left Cauchy–Green deformation tensor in three-dimensions. Compatibility conditions for two-dimensional ${\boldsymbol {B}}$ fields have been found by Janet Blume.^[17]^[18]

References

1 2 Lubliner, Jacob (2008). Plasticity Theory (Revised Edition) (PDF). Dover Publications. ISBN 0-486-46290-0.
↑ A. Yavari, J.E. Marsden, and M. Ortiz, On spatial and material covariant balance laws in elasticity, Journal of Mathematical Physics, 47, 2006, 042903; pp. 1–53.
↑ Owens, Eduardo de Souza Neto, Djordje Peric, David (2008). Computational methods for plasticity : theory and applications. Chichester, West Sussex, UK: Wiley. p. 65. ISBN 978-0-470-69452-7.
↑ The IUPAC recommends that this tensor be called the Cauchy strain tensor.
1 2 3 4 A. Kaye, R. F. T. Stepto, W. J. Work, J. V. Aleman (Spain), A. Ya. Malkin (1998). "Definition of terms relating to the non-ultimate mechanical properties of polymers". Pure & Appl. Chem. 70 (3): 701–754. doi:10.1351/pac199870030701.
↑ Eduardo N. Dvorkin, Marcela B. Goldschmit, 2006 Nonlinear Continua, p. 25, Springer ISBN 3-540-24985-0.
↑ The IUPAC recommends that this tensor be called the Green strain tensor.
↑ Jirásek,Milan; Bažant, Z. P. (2002) Inelastic analysis of structures, Wiley, p. 463 ISBN 0-471-98716-6
↑ J. N. Reddy, David K. Gartling (2000) The finite element method in heat transfer and fluid dynamics, p. 317, CRC Press ISBN 1-4200-8598-0.
↑ Belytschko, Ted; Liu, Wing Kam; Moran, Brian (2000). Nonlinear Finite Elements for Continua and Structures (reprint with corrections, 2006 ed.). John Wiley & Sons Ltd. pp. 92–94. ISBN 978-0-471-98773-4.
↑ Seth, B. R. (1961), "Generalized strain measure with applications to physical problems", MRC Technical Summary Report #248, Mathematics Research Center, United States Army, University of Wisconsin: 1–18.
↑ Seth, B. R. (1962), "Generalized strain measure with applications to physical problems", IUTAM Symposium on Second Order Effects in Elasticity, Plasticity and Fluid Mechanics, Haifa, 1962.
↑ Hill, R. (1968), "On constitutive inequalities for simple materials—I", Journal of the Mechanics and Physics of Solids, 16 (4): 229–242., Bibcode:1968JMPSo..16..229H, doi:10.1016/0022-5096(68)90031-8
↑ T.C. Doyle and J.L. Eriksen (1956). "Non-linear elasticity." Advances in Applied Mechanics 4, 53–115.
↑ Z.P. Bažant and L. Cedolin (1991). Stability of Structures. Elastic, Inelastic, Fracture and Damage Theories. Oxford Univ. Press, New York (2nd ed. Dover Publ., New York 2003; 3rd ed., World Scientific 2010).
↑ Z.P. Bažant (1998). "Easy-to-compute tensors with symmetric inverse approximating Hencky finite strain and its rate." J. of Materials of Technology ASME, 120 (April), 131–136.
↑ Blume, J. A. (1989). "Compatibility conditions for a left Cauchy–Green strain field". J. Elasticity. 21: 271–308. doi:10.1007/BF00045780.
↑ Acharya, A. (1999). "On Compatibility Conditions for the Left Cauchy–Green Deformation Field in Three Dimensions" (PDF). Journal of Elasticity. 56 (2): 95–105. doi:10.1023/A:1007653400249.

External links

Prof. Amit Acharya's notes on compatibility on iMechanica

This article is issued from Wikipedia - version of the 11/11/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.