Finite character

In mathematics, a family 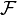$\mathcal{F}$ of sets is of finite character provided it has the following properties:

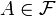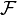For each $A\in \mathcal{F}$ , every finite subset of $A$ belongs to $\mathcal{F}$ .
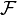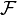If every finite subset of a given set $A$ belongs to $\mathcal{F}$ , then $A$ belongs to $\mathcal{F}$ .

Properties

A family 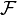$\mathcal{F}$ of sets of finite character enjoys the following properties:

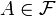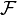For each $A\in \mathcal{F}$ , every (finite or infinite) subset of $A$ belongs to $\mathcal{F}$ .
Tukey's lemma: In 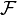$\mathcal{F}$ , partially ordered by inclusion, the union of every chain of elements of 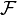$\mathcal{F}$ also belong to 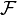$\mathcal{F}$ , therefore, by Zorn's lemma, 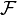$\mathcal{F}$ contains at least one maximal element.

Example

Let V be a vector space, and let F be the family of linearly independent subsets of V. Then F is a family of finite character (because a subset X ⊆ V is linearly dependent iff X has a finite subset which is linearly dependent). Therefore, in every vector space, there exists a maximal family of linearly independent elements. As a maximal family is a vector basis, every vector space has a (possibly infinite) vector basis.

This article incorporates material from finite character on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia - version of the 3/14/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.