Ecliptic coordinate system
The ecliptic coordinate system is a celestial coordinate system commonly used for representing the positions and orbits of Solar System objects. Because most planets (except Mercury), and many small Solar System bodies have orbits with small inclinations to the ecliptic, using it as the fundamental plane is convenient. The system's origin can be either the center of the Sun or the center of the Earth, its primary direction is towards the vernal (northbound) equinox, and it has a right-handed convention. It may be implemented in spherical coordinates or rectangular coordinates.[1]
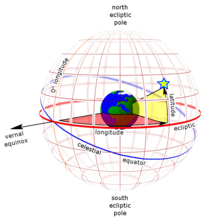
Primary direction

The celestial equator and the ecliptic are slowly moving due to perturbing forces on the Earth, therefore the orientation of the primary direction, their intersection at the Northern Hemisphere vernal equinox, is not quite fixed. A slow motion of Earth's axis, precession, causes a slow, continuous turning of the coordinate system westward about the poles of the ecliptic, completing one circuit in about 26,000 years. Superimposed on this is a smaller motion of the ecliptic, and a small oscillation of the Earth's axis, nutation.[2][3]
In order to reference a coordinate system which can be considered as fixed in space, these motions require specification of the equinox of a particular date, known as an epoch, when giving a position in ecliptic coordinates. The three most commonly used are:
- Mean equinox of a standard epoch (usually J2000.0, but may include B1950.0, B1900.0, etc.)
- is a fixed standard direction, allowing positions established at various dates to be compared directly.
- Mean equinox of date
- is the intersection of the ecliptic of "date" (that is, the ecliptic in its position at "date") with the mean equator (that is, the equator rotated by precession to its position at "date", but free from the small periodic oscillations of nutation). Commonly used in planetary orbit calculation.
- True equinox of date
- is the intersection of the ecliptic of "date" with the true equator (that is, the mean equator plus nutation). This is the actual intersection of the two planes at any particular moment, with all motions accounted for.
A position in the ecliptic coordinate system is thus typically specified true equinox and ecliptic of date, mean equinox and ecliptic of J2000.0, or similar. Note that there is no "mean ecliptic", as the ecliptic is not subject to small periodic oscillations.[4]
Spherical coordinates
| Spherical | Rectangular | |||
|---|---|---|---|---|
| Longitude | Latitude | Distance | ||
| Geocentric | λ | β | Δ | |
| Heliocentric | l | b | r | x, y, z[note 1] |
| ||||
Ecliptic longitude or celestial longitude (symbols: heliocentric , geocentric ) measures the angular distance of an object along the ecliptic from the primary direction. Like right ascension in the equatorial coordinate system, the primary direction (0° ecliptic longitude) points from the Earth towards the Sun at the vernal equinox of the Northern Hemisphere. Because it is a right-handed system, ecliptic longitude is measured positive eastwards in the fundamental plane (the ecliptic) from 0° to 360°. Because of axial precession, the ecliptic longitude of most "fixed stars" (referred to the equinox of date) increases by about 50.3 arcseconds per year, or 83.8 arcminutes per century, the speed of general precession.[6][7] However, for stars near the ecliptic poles, the rate of change of ecliptic longitude is dominated by the slight movement of the ecliptic (that is, of the plane of the earth's orbit), so the rate of change may be anything from minus infinity to plus infinity depending on the exact position of the star.
Ecliptic latitude or celestial latitude (symbols: heliocentric , geocentric ), measures the angular distance of an object from the ecliptic towards the north (positive) or south (negative) ecliptic pole. For example, the north ecliptic pole has a celestial latitude of +90°. Ecliptic latitude for "fixed stars" is not affected by precession.
Distance is also necessary for a complete spherical position (symbols: heliocentric , geocentric ). Different distance units are used for different objects. Within the Solar System, astronomical units are used, and for objects near the Earth, Earth radii or kilometers are used.
Historical usage
From antiquity through the 18th century, ecliptic longitude was commonly measured using twelve zodiacal signs, each of 30° longitude, a usage that continues in modern astrology. The signs approximately corresponded to the constellations crossed by the ecliptic. Longitudes were specified in signs, degrees, minutes, and seconds. For example, a longitude of ![]() 19° 55′ 58″ is 19.933° east of the start of the sign Leo. Since Leo begins 120° from the vernal equinox, the longitude in modern form is 139° 55′ 58″.[8]
19° 55′ 58″ is 19.933° east of the start of the sign Leo. Since Leo begins 120° from the vernal equinox, the longitude in modern form is 139° 55′ 58″.[8]
In China, ecliptic longitude is measured using 24 Solar terms, each of 15° longitude, and are used by Chinese lunisolar calendars to stay synchronized with the seasons, which is crucial for agrarian societies.
Rectangular coordinates
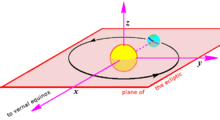
A rectangular variant of ecliptic coordinates is often used in orbital calculations and simulations. It has its origin at the center of the Sun (or at the barycenter of the solar system), its fundamental plane in the plane of the ecliptic, and the x axis toward the vernal equinox. The coordinates have a right-handed convention, that is, if one extends their right thumb upward, it simulates the z-axis, their extended index finger the x-axis, and the curl of the other fingers points generally in the direction of the y-axis.[9]
These rectangular coordinates are related to the corresponding spherical coordinates by
- .
Conversion between celestial coordinate systems
Converting Cartesian vectors
Conversion from ecliptic coordinates to equatorial coordinates
Conversion from equatorial coordinates to ecliptic coordinates
where is the obliquity of the ecliptic.
See also
- Celestial coordinate system
- Ecliptic
- Ecliptic poles, where the ecliptic latitude is ±90°
- Equinox
Notes and references
- ↑ Nautical Almanac Office, U.S. Naval Observatory; H.M. Nautical Almanac Office, Royal Greenwich Observatory (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office, London. pp. 24–27.
- ↑ Explanatory Supplement (1961), pp. 20, 28
- ↑ U.S. Naval Observatory, Nautical Almanac Office (1992). P. Kenneth Seidelmann, ed. Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley, CA. pp. 11–13. ISBN 0-935702-68-7.
- ↑ Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. p. 137. ISBN 0-943396-35-2.
- ↑ Explanatory Supplement (1961), sec. 1G
- ↑ N. Capitaine; P.T. Wallace; J. Chapront (2003). "Expressions for IAU 2000 precession quantities" (PDF). Astronomy & Astrophysics: 581. doi:10.1051/0004-6361:20031539.
- ↑ J.H. Lieske et al. (1977), "Expressions for the Precession Quantities Based upon the IAU (1976) System of Astronomical Constants". Astronomy & Astrophysics 58, pp. 1-16
- ↑ Leadbetter, Charles (1742). A Compleat System of Astronomy. J. Wilcox, London. p. 94.; numerous examples of this notation appear throughout the book.
- ↑ Explanatory Supplement (1961), pp. 20, 27
- ↑ Explanatory Supplement (1992), pp. 555-558
External links
- The Ecliptic: the Sun's Annual Path on the Celestial Sphere Durham University Department of Physics
- MEASURING THE SKY A Quick Guide to the Celestial Sphere James B. Kaler, University of Illinois