Doob–Dynkin lemma
In probability theory, the Doob–Dynkin lemma, named after Joseph L. Doob and Eugene Dynkin, characterizes the situation when one random variable is a function of another by the inclusion of the 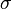 generated by the random variables. The usual statement of the lemma is formulated in terms of one random variable being measurable with respect to the
generated by the random variables. The usual statement of the lemma is formulated in terms of one random variable being measurable with respect to the 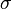 -algebra generated by the other.
-algebra generated by the other.
The lemma plays an important role in the conditional expectation in probability theory, where it allows to replace the conditioning on a random variable by conditioning on the 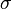 -algebra that is generated by the random variable.
-algebra that is generated by the random variable.
Statement of the lemma
Let 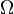 be a sample space. For a function
be a sample space. For a function  , the
, the 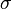 -algebra generated by
-algebra generated by  is defined as the family of sets
is defined as the family of sets 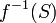 , where
, where 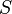 are all Borel sets.
are all Borel sets.
Lemma Let 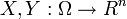 be random elements and
be random elements and 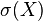 be the
be the 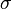 algebra generated by
algebra generated by 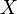 . Then
. Then 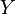 is
is 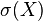 -measurable if and only if
-measurable if and only if  for some Borel measurable function
for some Borel measurable function 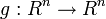 .
.
The "if" part of the lemma is simply the statement that the composition of two measurable functions is measurable. The "only if" part is the nontrivial one.
By definition, 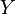 being
being 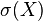 -measurable is the same as
-measurable is the same as 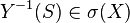 for any Borel set
for any Borel set 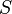 , which is the same as
, which is the same as 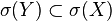 . So, the lemma can be rewritten in the following, equivalent form.
. So, the lemma can be rewritten in the following, equivalent form.
Lemma Let 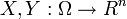 be random elements and
be random elements and 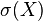 and
and 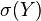 the
the 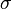 algebras generated by
algebras generated by 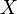 and
and 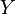 , respectively. Then
, respectively. Then  for some Borel measurable function
for some Borel measurable function 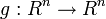 if and only if
if and only if 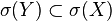 .
.
References
- A. Bobrowski: Functional analysis for probability and stochastic processes: an introduction, Cambridge University Press (2005), ISBN 0-521-83166-0
- M. M. Rao, R. J. Swift : Probability Theory with Applications, Mathematics and Its Applications, Band 582, Springer-Verlag (2006), ISBN 0-387-27730-7