Asymmetric Numeral Systems

Asymmetric Numeral Systems (ANS) ^[1] is a family of entropy coding methods used in data compression since 2014^[2] for example in the Facebook Zstandard compressor^[3] and Apple LZFSE compressor,^[4] due to improved performance compared to the previously used methods: it allows combination of the compression ratio of arithmetic coding (uses nearly accurate probability distribution), with a processing cost similar to Huffman coding (tANS variant constructs finite state machine to operate on large alphabet without using multiplication).

The basic concept is to directly encode information into a single natural number $x$ , increased approximately $1/p$ times while adding information from symbol of probability $p$ . For the encoding rule, the set of natural numbers is split into disjoint subsets corresponding to different symbols - like into even and odd numbers, but with densities corresponding to the probability distribution of symbols to encode. Then to add information from symbol $s$ into information already stored in the current number $x$ , we go to number $x'=C(x,s)\approx x/p$ being position of $x$ -th appearances from $s$ -th subset.

There are alternative ways to apply it in practice - direct mathematical formulas for encoding and decoding steps (uABS and rANS variants), or one can put the entire behavior into a table (tANS variant). Renormalization is used to prevent $x$ going to infinity - transferring accumulated bits to or from the bitstream.

Basic concepts

Comparison of the concept of arithmetic coding (left) and ANS (right). Both can be seen as generalization of standard numeral systems, optimal for uniform probability distribution of digits, into optimized for some chosen probability distribution. Arithmetic or range coding corresponds to adding new information in the most significant position, while ANS generalizes adding information in the least significant position. Its coding rule is "x goes to x-th appearance of subset of natural numbers corresponding to currently encoded symbol". In the presented example, sequence (01111) is encoded into a natural number 18, which is smaller than 45 obtained by using standard binary system, due to better agreement with frequencies of sequence to encode. The advantage of ANS is storing information in a single natural number, in contrast to two defining a range.

Imagine there is some information stored in a natural number $x$ , for example as bit sequence of its binary expansion. To add information from a binary variable $s$ , we can use coding function $x'=C(x,s)=2x+s$ , which shifts all bits one position up, and place the new bit in the least significant position. Now decoding function $D(x')=(\lfloor x'/2\rfloor ,\mathrm {mod} (x',2))$ allows to retrieve the previous $x$ and this added bit: $D(C(x,s))=(x,s),\ C(D(x'))=x'$ . We can start with $x=1$ initial state, then use the $C$ function on the successive bits of a finite bit sequence to obtain a final $x$ number storing this entire sequence. Then using $D$ function multiple times until $x=1$ allows to retrieve the bit sequence in reversed order.

The above procedure is optimal for uniform (symmetric) probability distribution of symbols $\Pr(0)=\Pr(1)=1/2$ . ANS generalize it to make it optimal for any chosen (asymmetric) probability distribution of symbols: $\Pr(s)=p_{s}$ . While $s$ in the above example was choosing between even and odd $C(x,s)$ , in ANS this even/odd division of natural numbers is replaced with division into subsets having densities corresponding to the assumed probability distribution $\{p_{s}\}_{s}$ : up to position $x$ , there is approximately $xp_{s}$ occurrences of symbol $s$ .

The coding function $C(x,s)$ returns the $x$ -th appearance from such subset corresponding to symbol $s$ . The density assumption is equivalent to condition $x'=C(x,s)\approx x/p_{s}$ . Assuming that a natural number $x$ contains $\log _{2}(x)$ bits information, $\log _{2}(C(x,s))\approx \log _{2}(x)+\log _{2}(1/p_{s})$ . Hence the symbol of probability $p_{s}$ is encoded as containing $\approx \log _{2}(1/p_{s})$ bits of information as it is required from entropy coders.

Uniform binary variant (uABS)

Let us start with binary alphabet and probability distribution $\Pr(1)=p,\Pr(0)=1-p$ . Up to position $x$ we want approximately $p\cdot x$ analogues of odd numbers (for $s=1$ ). We can choose this number of appearances as $\lceil x\cdot p\rceil$ , getting $s=\lceil (x+1)\cdot p\rceil -\lceil x\cdot p\rceil$ . This is called uABS variant and leads to the following decoding and encoding functions:^[5]

Decoding:

s = ceil((x+1)*p) - ceil(x*p)  // 0 if fract(x*p) < 1-p, else 1
if s = 0 then new_x = x - ceil(x*p)   // D(x) = (new_x, 0)
if s = 1 then new_x = ceil(x*p)  // D(x) = (new_x, 1)

Encoding:

if s = 0 then new_x = ceil((x+1)/(1-p)) - 1 // C(x,0) = new_x
if s = 1 then new_x = floor(x/p)  // C(x,1) = new_x

For $p=1/2$ it becomes standard binary system (with switched 0 and 1), for a different $p$ it becomes optimal for this given probability distribution. For example, for $p=0.3$ these formulas lead to table for small values of $x$ :

$C(x,s)$	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
$s=0$		0	1		2	3		4	5	6		7	8		9	10		11	12	13
$s=1$	0			1			2				3			4			5				6

Symbol $s=1$ corresponds to subset of natural numbers of density $p=0.3$ , which in this case are positions $\{0,3,6,10,13,16,20,23,26,\ldots \}$ . As $1/4<0.3<1/3$ , these positions increase by 3 or 4. Because $p=3/10$ here, the pattern of symbols repeats every 10 positions.

The $C(x,s)$ can be found by taking row corresponding to a given symbol $s$ , and take given $x$ in this row. Then top row provides $C(x,s)$ . For example, $C(7,0)=11$ from the middle to top row.

Imagine we would like to encode '0100' sequence starting from $x=1$ . First $s=0$ takes us to $x=2$ , then $s=1$ to $x=6$ , then $s=0$ to $x=9$ , then $s=0$ to $x=14$ . By using decoding function $D(x')$ on this final $x$ , we can retrieve the symbol sequence. Using the table for this purpose, $x$ in first row determines column, then nonempty row and the written value determine correspondingly $s$ and $x$ .

Range variants (rANS) and streaming

Range variant also uses arithmetic formulas, but allows to operate on large alphabet. Intuitively, it divides the set of natural numbers into size $2^{n}$ ranges, and split each of them in identical way into subranges of proportions given by the assumed probability distribution.

We start with quanization of probability distribution to $2^{n}$ denominator, where $n$ is chosen (usually 8-12 bits): $p_{s}\approx f[s]/2^{n}$ for some natural $f[s]$ numbers (sizes of subranges).

Denote ${\text{mask}}=2^{n}-1$ , cumulative distribution function: $\operatorname {CDF} [s]=\sum _{i<s}f[i]=f[0]+\ldots +f[s-1]$ .

For $y\in [0,2^{n}-1]$ denote function (usually tabled)

symbol(y) = s such that CDF[s] <= y < CDF[s+1] .

Now coding function is:

C(x,s) = floor(x / f[s]) << n) + (x % f[s]) + CDF[s]

Decoding: s = symbol(x & mask)

D(x) = (f[s] * (x >> n) + (x & mask ) - CDF[s], s)

This way we can encode a sequence of symbols into a large natural number $x$ . To avoid using large number arithmetic, in practice stream variants are used: which enforce $x\in [L,b\cdot L-1]$ by renormalization: sending the least significant bits of $x$ to or from the bitstream (usually $L$ and $b$ are powers of 2).

In rANS variant $x$ is for example 32 bit. For 16 bit renormalization, $x\in [2^{16},2^{32}-1]$ , decoder refills the least significant bits from the bitstream when needed:

if(x < (1 << 16)) x = (x << 16) + read16bits()

Tabled variant (tANS)

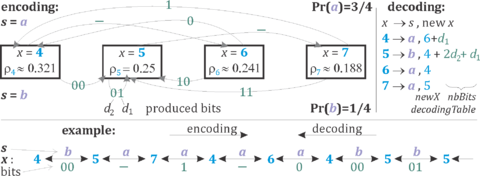
Simple example of 4 state ANS automaton for Pr(a) = 3/4, Pr(b) = 1/4 probability distribution. Symbol b contains −lg(1/4) = 2 bits of information and so it always produces two bits. In contrast, symbol a contains −lg(3/4) ~ 0.415 bits of information, hence sometimes it produces one bit (from state 6 and 7), sometimes 0 bits (from state 4 and 5), only increasing the state, which acts as buffer containing fractional number of bits: lg(x). The number of states in practice is for example 2048, for 256 size alphabet (to directly encode bytes).

tANS variant puts the entire behavior (including renormalization) for $x\in [L,2L-1]$ into a table, getting finite state machine avoiding the need of multiplication.

Finally step of decoding loop can be written as:

t = decodingTable(x);  
x = t.newX + readBits(t.nbBits); //state transition
writeSymbol(t.symbol); //decoded symbol

Step of encoding loop:

s = ReadSymbol();
nbBits = (x + ns[s]) >> r;  // # of bits for renormalization
writeBits(x, nbBits);  // send youngest bits to bitstream
x = encodingTable[start[s] + (x >> nbBits)];

A specific tANS coding is determined by assigning a symbol to every $[L,2L-1]$ position, their number of appearances should be proportional to the assumed probabilities. For example one could choose "abdacdac" assignment for Pr(a)=3/8, Pr(b)=1/8, Pr(c)=2/8, Pr(d)=2/8 probability distribution. If symbols are assigned in ranges of lengths being powers of 2, we would get Huffman coding. For example a->0, b->100, c->101, d->11 prefix code would be obtained for tANS with "aaaabcdd" symbol assignment.

Remarks

As for Huffman coding, modifying the probability distribution of tANS is costly, hence they are used in static situations, usually with some Lempel–Ziv scheme (ZSTD, LZFSE). In this case, the file is divided into blocks and static probability distribution for each block is stored in its header.

In contrast, rANS is usually used as faster replacement for range coding. It requires multiplication, but is more memory efficient and is appropriate for dynamically adapting probability distributions.

Encoding and decoding of ANS are performed in opposite directions. This inconvenience is usually resolved by encoding in backward direction, thanks of it decoding can made forward. For context-dependence, like Markov model, the encoder needs to use context from the perspective of decoder. For adaptivity, the encoder should first go forward to find probabilities which will be used by decoder and store them in a buffer, then encode in backward direction using the found probabilities.

The final state of encoding is required to start decoding, hence it needs to be stored in the compressed file. This cost can be compensated by storing some information in the initial state of encoder.

References

↑ J. Duda, K. Tahboub, N. J. Gadil, E. J. Delp, The use of asymmetric numeral systems as an accurate replacement for Huffman coding, Picture Coding Symposium, 2015.
↑ List of compressors using ANS, implementations and other materials
↑ Smaller and faster data compression with Zstandard, Facebook, August 2016
↑ Apple Open-Sources its New Compression Algorithm LZFSE, InfoQ, July 2016
↑ Data Compression Explained, Matt Mahoney

External links

High throughput hardware architectures for asymmetric numeral systems entropy coding S. M. Najmabadi, Z. Wang, Y. Baroud, S. Simon, ISPA 2015
https://github.com/Cyan4973/FiniteStateEntropy Finite state entropy (FSE) implementation of tANS by Yann Collet
https://github.com/rygorous/ryg_rans Implementation of rANS by Fabian Giesen
https://github.com/jkbonfield/rans_static Fast implementation of rANS and aritmetic coding by James K. Bonfield
https://github.com/facebook/zstd/ Facebook Zstandard compressor by Yann Collet (author of LZ4)
https://github.com/lzfse/lzfse LZFSE compressor (LZ+FSE) of Apple Inc.
CRAM 3.0 DNA compressor (order 1 rANS) (part of SAMtools) by European Bioinformatics Institute
https://chromium-review.googlesource.com/#/c/318743 implementation for Google VP10
https://chromium-review.googlesource.com/#/c/338781/ implementation for Google WebP
https://aomedia.googlesource.com/aom/+/master/aom_dsp implementation of Alliance for Open Media
http://demonstrations.wolfram.com/DataCompressionUsingAsymmetricNumeralSystems/ Wolfram Demonstrations Project
http://gamma.cs.unc.edu/GST/ GST: GPU-decodable Supercompressed Textures
Understanding compression book by A. Haecky, C. McAnlis

Data compression methods

Lossless

Entropy type	Unary Arithmetic Asymmetric Numeral Systems Golomb Huffman Adaptive Canonical Modified Range Shannon Shannon–Fano Shannon–Fano–Elias Tunstall Universal Exp-Golomb Fibonacci Gamma Levenshtein

Dictionary type	Byte pair encoding DEFLATE Snappy Lempel–Ziv LZ77 / LZ78 (LZ1 / LZ2) LZJB LZMA LZO LZRW LZS LZSS LZW LZWL LZX LZ4 Brotli Statistical

Other types	BWT CTW Delta DMC MTF PAQ PPM RLE

Audio

Concepts	Bit rate average (ABR) constant (CBR) variable (VBR) Companding Convolution Dynamic range Latency Nyquist–Shannon theorem Sampling Sound quality Speech coding Sub-band coding

Codec parts	A-law μ-law ACELP ADPCM CELP DPCM Fourier transform LPC LAR LSP MDCT Psychoacoustic model WLPC

Image

Concepts	Chroma subsampling Coding tree unit Color space Compression artifact Image resolution Macroblock Pixel PSNR Quantization Standard test image

Methods	Chain code DCT EZW Fractal KLT LP RLE SPIHT Wavelet

Video

Concepts	Bit rate average (ABR) constant (CBR) variable (VBR) Display resolution Frame Frame rate Frame types Interlace Video characteristics Video quality

Codec parts	Lapped transform DCT Deblocking filter Motion compensation

Theory

Compression formats
Compression software (codecs)

This article is issued from Wikipedia - version of the 11/29/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.